Hình bên là đồ thị của ba hàm số y = a^x, y = b^x, y = c^x (0 < a, b, c khác 1) được vẽ
Câu hỏi:
Hình bên là đồ thị của ba hàm số y = ax, y = bx, y = cx (0 < a, b, c ≠ 1) được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
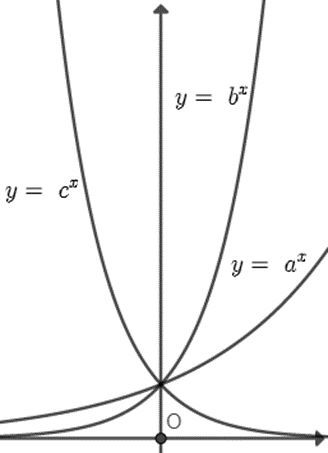
A. a > b > c;
B. c > b > a;
C. a > c > b;
D. b > a > c.
Trả lời:
Đáp án đúng là: D.
Đồ thị hàm số y = cx có dạng đi xuống nên 0 < c < 1.
Đồ thị hàm số y = bx; y = ax có dạng đi lên và đồ thị y = bx nằm phía trên đồ thị hàm số y = ax nên b > a > 1.
Do đó ta có b > a > c.

