Miền nghiệm của hệ bất phương trình 2x + 3y - 6 < 0; x > = 0; 2x - 3y - 1 < = 0
Câu hỏi:
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?
A. A(1; 2);
B. B(0; 2);
C. C(−1; 3);
D. \(D\left( {0;\; - \frac{1}{3}} \right)\).
Trả lời:
Đáp án đúng là: D
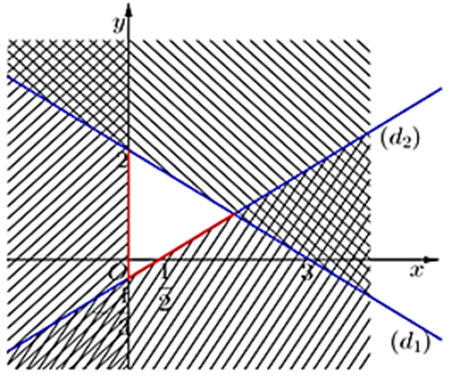
Trước hết, ta vẽ ba đường thẳng:
(d1): 2x + 3y − 6 = 0
(d2): x = 0
(d3): 2x − 3y − 1 = 0
Ta thấy (1; 1) là nghiệm của các ba bất phương trình.
Điều này có nghĩa là điểm (1; 1) thuộc cả ba miền nghiệm của ba bất phương trình.
Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Vậy trong tất cả các đáp án, chỉ có một điểm thuộc miền nghiệm của hệ phương trình là: \(D\left( {0;\; - \frac{1}{3}} \right)\).