Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình
Câu hỏi:
Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn bệ A, B, C, D?
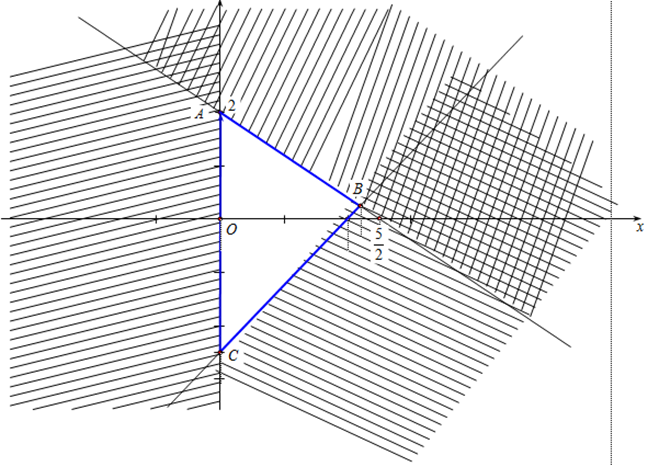
A. \(\left\{ \begin{array}{l}y \ge 0\\5{\rm{x}} - 4y \ge 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x \ge 0\\{\rm{4x}} - 5y \le 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x \ge 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x > 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\).
Trả lời:
Đáp án đúng là C
Dựa vào hình vẽ, ta thấy
Đường thẳng (d1) là trục tung \({\rm{Oy}}\) nên có phương trình x = 0
Đường thẳng (d2) đi qua hai điểm (0; 2) và \(\left( {\frac{5}{2};0} \right)\) nên có phương trình
\(\frac{x}{{\frac{5}{2}}} + \frac{y}{2} = 1 \Leftrightarrow \frac{{2x}}{5} + \frac{y}{2} = 1 \Leftrightarrow 4x + 5y = 10\)
Đường thẳng (d3) đi qua các điềm (2; 0) và \(\left( {0; - \frac{5}{2}} \right)\) nên có phương trình
\(\frac{x}{2} + \frac{y}{{ - \frac{5}{2}}} = 1 \Leftrightarrow \frac{x}{2} - \frac{{2y}}{5} = 1 \Leftrightarrow 5x - 4y = 10\)
Miền nghiệm gần phần mặt phẳng nhận giá trị x dương (kể cả bờ (d1))
Lại có (0; 0) là nghiệm của cả hai bất phương trình 4x + 5y ≤ 10 và 5x – 4y ≤ 10
Suy ra miền tam giác ABC biểu diễn nghiệm của hệ \(\left\{ \begin{array}{l}x \ge 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\)
Vậy ta chọn đáp án C.

