Một công ty điện tử sản suất hai loại máy tính trên hai dây chuyền độc lập (loại
Câu hỏi:
Một công ty điện tử sản suất hai loại máy tính trên hai dây chuyền độc lập (loại một và loại hai). Máy tính loại một sản xuất trên dây chuyền một với công suất tối đa 45 máy tính một ngày; máy tính loại hai sản xuất trên dây chuyền hai với công suất tối đa 80 máy tính một ngày. Để sản xuất một chiếc máy tính loại một cần 12 linh kiện và cần 9 linh kiện để sản xuất một máy tính loại hai. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900 linh kiện và tiền lãi bán một chiếc máy loại một là 250.000 đồng; tiền lãi khi bán một chiếc máy loại hai là 180.000 đồng. Hỏi cần sản xuất mỗi loại bao nhiêu máy tính để tiền lãi thu được trong một ngày là nhiều nhất. (Giả thiết rằng tất cả các máy tính sản xuất ra trong ngày đều bán hết).
Trả lời:
Gọi số máy tính kiểu một và kiểu hai mà công ty này sản xuất trong một ngày lần lượt là x, y (x, y ∈ ℕ*, chiếc).
Số tiền lãi công ty thu được trong 11 ngày:
F(x; y) = 250x + 180y (nghìn đồng)
Công suất của dây chuyền 1 là 45 máy tính/ngày và dây chuyền 2 là 80 máy tính/ngày
Suy ra: \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\end{array} \right.\)
Để sản xuất 1 chiếc máy tính kiểu một cần 12 linh kiện điện tử A và một chiếc máy tính kiểu hai cần 9 linh kiện này. Số linh kiện này được cung cấp mỗi ngày không quá 900
⇒ 12x + 9y ≤ 900
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\12x + 9y \le 900\end{array} \right.\)
Miền của hệ BPT là phần mặt phẳng đậm nhất trong hình, kể cả biên
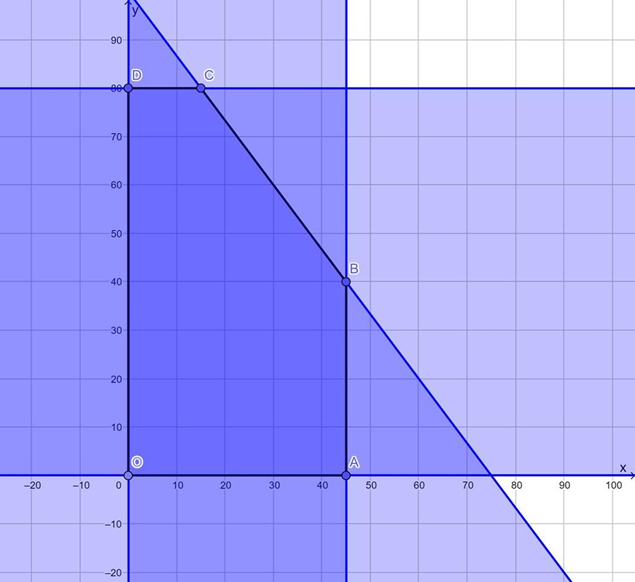
F(x; y) đạt GTLN khi (x; y) là một trong số các điểm A(45; 0), B(45; 40), C(15; 80), D(0; 80).
Thay vào hàm F(x; y) ta có F(x; y) đạt GTLN bằng 18450 (nghìn đồng) khi (x; y) = (45; 40).
Vậy cần sản xuất loại 1 là 45 chiếc, loại 2 là 40 chiếc.

