Một hình trụ có bán kính đáy R = 70 cm, chiều cao hình trụ h = 20 cm. Một hình vuông
Câu hỏi:
Một hình trụ có bán kính đáy R = 70 cm, chiều cao hình trụ h = 20 cm. Một hình vuông có các đỉnh nằm trên hai đường tròn đáy sao cho có ít nhất một cạnh không song song và không vuông góc với trục hình trụ. Khi đó cạnh của hình vuông bằng bao nhiêu?
A. 80 cm
B. 100 cm
C. \(100\sqrt 2 \) cm
D. 140 cm.
Trả lời:
Đáp án đúng là: B
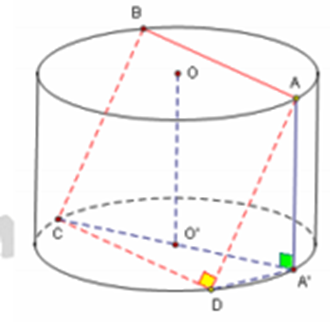
Xét hình vuông có cạnh AD không song song và vuông góc với trục OO’ của hình trụ. Vẽ đường sinh AA’
Ta có CD ⊥ (AA’D) suy ra CD ⊥ A’D nên tam giác A’CD vuông tại D
Hay A’C là đường kính của đường tròn đáy
Suy ra A’C = 2 . 70 = 140 cm
Vì tam giác AA’C vuông tại A’ nên theo Pytago có
\[{\rm{A}}C = \sqrt {A'{A^2} + A'{C^2}} = \sqrt {{{20}^2} + {{140}^2}} = 100\sqrt 2 \]cm
Vì \[{\rm{A}}C = AB\sqrt 2 \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = 100cm\]
Vậy ta chọn đáp án B.


