Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x^3 - 3x^2 + 1

❮ Bài trước Bài sau ❯

Câu hỏi:

Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = x^{3} - 3 x^{2} + 1$ là:

A. $y = - 2 x + 1$

B. $y = 2 x - 1$

C. $y = - 2 x - 1$

D. $y = 2 x + 1$

Trả lời:

Đáp án A

$y' = 3 x^{2} - 6 x y' = 0 \Leftrightarrow 3 x (x - 2) = 0 \Leftrightarrow [\begin{matrix} x = 0 \Rightarrow y = 1 \\ x = 2 \Rightarrow y = - 3 \end{matrix}$

Từ đây suy ra hai điểm cực trị có tọa độ A (0; 1) và B (2; - 3)

Phương trình đường thẳng qua hai điểm A, B là:

$\frac{x - 0}{2 - 0} = \frac{y - 1}{- 3 - 1} \Leftrightarrow - 4 x = 2 (y - 1) \Leftrightarrow y = - 2 x + 1$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số y = f(x) có bảng biến thiên sau:

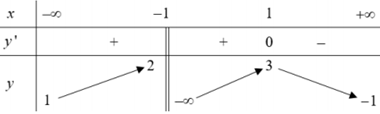
Khẳng định nào sau đây sai?

Xem lời giải »

Câu 2:

Số điểm cực trị của đồ thị hàm số $y = \frac{x - 1}{2 - x}$ là:

Xem lời giải »

Câu 3:

Hàm số $y = x^{4} + 2 x^{3} - 2017$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 4:

Số điểm cực trị của hàm số $y = \frac{5 x - 1}{x + 2}$

Xem lời giải »

Câu 5:

Gọi $A (x_{1}; y_{1}), B (x_{2}; y_{2})$ là hai điểm cực trị của đồ thị hàm số $y = \frac{1}{3} x^{3} - 4 x^{2} - x + 4$ . Tính $P = \frac{y_{1} - y_{2}}{x_{1} - x_{2}}$