Hàm số f(x) = 2sin2x - 3 đạt cực tiểu tại: x = pi/4 + k.pi

❮ Bài trước Bài sau ❯

Câu hỏi:

Hàm số $f (x) = 2 \sin 2 x - 3$ đạt cực tiểu tại:

A. $x = \frac{π}{4} + k π$

B. $x = \frac{π}{4} + \frac{k π}{2}$

C. $x = \frac{π}{2} + k π$

D. $x = \frac{π}{4} + \frac{(2 k + 1) π}{2}$

Trả lời:

Đáp án D

Ta có: $f (x) = 2 \sin 2 x - 3$

TXĐ: D = R

$f' (x) = 4 \cos 2 x; f' (x) = 0 \Leftrightarrow \cos 2 x = 0 \Leftrightarrow 2 x = \frac{π}{2} + k π \Leftrightarrow x = \frac{π}{4} + \frac{k π}{2}, k \in Z f'' (x) = - 8 \sin 2 x$

Ta có: $f'' (\frac{π}{4} + \frac{k π}{2}) = - 8 \sin (\frac{π}{2} + k π), k \in Z$

Khi $k = 2 n \Rightarrow \sin (\frac{π}{2} + 2 n π) = \sin \frac{π}{2} = 1$ nên $f'' (\frac{π}{4} + \frac{2 n π}{2}) = - 8 < 0$

Khi $k = 2 n + 1 \Rightarrow \sin (\frac{π}{2} + (2 n + 1) π) = \sin \frac{3 π}{2} = - 1$ nên $f'' (\frac{π}{4} + \frac{(2 n + 1) π}{2}) = 8 > 0$

Vậy hàm số đạt cực tiểu tại $x = \frac{π}{4} + \frac{(2 k + 1) π}{2}$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số y = f(x) có bảng biến thiên sau:

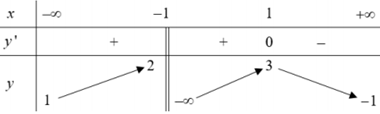
Khẳng định nào sau đây sai?

Xem lời giải »

Câu 2:

Số điểm cực trị của đồ thị hàm số $y = \frac{x - 1}{2 - x}$ là:

Xem lời giải »

Câu 3:

Hàm số $y = x^{4} + 2 x^{3} - 2017$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 4:

Số điểm cực trị của hàm số $y = \frac{5 x - 1}{x + 2}$

Xem lời giải »

Câu 5:

Đồ thị hàm số nào sau đây có 3 điểm cực trị?

Xem lời giải »

Câu 6:

Hàm số $y = {(x^{3} - 3 x)}^{e}$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 7:

Hàm số $y = - 2 x^{4} + 4 x^{2} + 5$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 8:

Cho hàm số y = f(x) có đạo hàm $f' (x) = (x - 1) (x^{2} - 2) (x^{4} - 4)$ . Số điểm cực trị của hàm số y = f(x) là:

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Hàm số f(x) = 2sin2x - 3 đạt cực tiểu tại: x = pi/4 + k.pi

Xem thêm bài tập Toán có lời giải hay khác: