Tìm m để phương trình x^5 + x^3 - căn (1 - x) + m = 0 có nghiệm trên

❮ Bài trước Bài sau ❯

Câu hỏi:

Tìm m để phương trình $x^{5} + x^{3} - \sqrt{1 - x} + m = 0$ có nghiệm trên $(- \infty; 1]$

A. $m \geq - 2$

B. m > 2

C. $m \leq - 2$

D. m < 2

Trả lời:

Đáp án A

Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C): $y = x^{5} + x^{3} - \sqrt{1 - x}$ và đường thẳng d: y = -m

Xét hàm số (C): $y = x^{5} + x^{3} - \sqrt{1 - x}$ có $y' = 5 x^{4} + 3 x^{2} + \frac{1}{2 \sqrt{1 - x}} > 0 \forall x \in (- \infty; 1) \Rightarrow$ hàm số luôn đồng biến trên $(- \infty; 1]$

Lại có y(1) = 2

Ta có BBT:

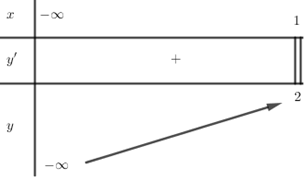
Theo BBT ta thấy phương trình có nghiệm $\Leftrightarrow - m \leq 2 \Leftrightarrow m \geq - 2$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hai đồ thị hàm số $y = x^{3} + 2 x^{2} - x + 1$ và đồ thị hàm số $y = x^{2} - x + 3$ có tất cả bao nhiêu điểm chung?

Xem lời giải »

Câu 2:

Cho hàm số y = f(x) xác định, liên tục trên R có BBT:

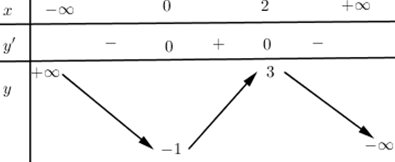
Bảng biến thiên trên là bảng biến thiên của hàm số nào?

Xem lời giải »

Câu 3:

Cho hàm số $y = f (x) = a x^{4} + b^{2} x^{2} + 1 (a > 0)$ . Trong các khẳng định dưới đây, khẳng định nào là sai?

Xem lời giải »

Câu 4:

Cho hàm số y = f(x) có bảng biến thiên như sau:

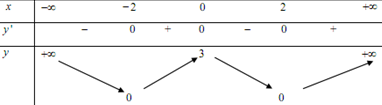
Khẳng định nào sau đây là khẳng định đúng?

Xem lời giải »

Câu 5:

Đồ thị hàm số nào sau đây có tiếp tuyến tại giao điểm của đồ thị và trục tung có hệ số góc âm?

Xem lời giải »

Câu 6:

Cho hàm số $y = x^{3} - 3 x^{2} + 5 x - 2$ có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) có hệ số góc nhỏ nhất

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Tìm m để phương trình x^5 + x^3 - căn (1 - x) + m = 0 có nghiệm trên

Xem thêm bài tập Toán có lời giải hay khác: