Tìm tất cả các giá trị của tham số m để hàm số y = -x^3 + 3x^2 + mx + 1 nghịch biến
Câu hỏi:
Tìm tất cả các giá trị của tham số m để hàm số y = −x3 + 3x2 + mx + 1 nghịch biến trên khoảng (0; +∞).
Trả lời:
Ta có: y = −x3 + 3x2 + mx + 1
Þ y¢ = −3x2 + 6x + m
Hàm số f (x) nghịch biến trên (0; +∞)
Û f ¢(x) ≤ 0, "x Î (0; +∞)
Û −3x2 + 6x + m ≤ 0, "x Î (0; +∞)
Û m ≤ 3x2 − 6x, "x Î (0; +∞) (*)
Xét hàm số y = g (x) = 3x2 − 6x trên (0; +∞).
g¢ (x) = 6x − 6 = 0 Û x = 1
Xét bảng biến thiên:
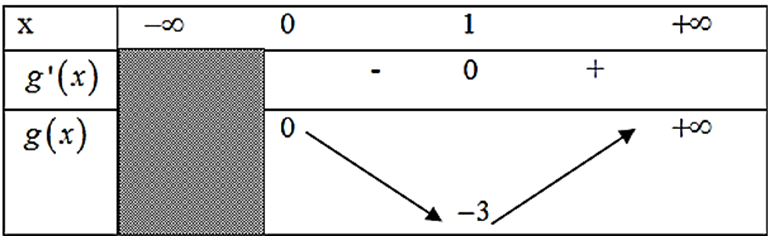
Do đó \(\left( * \right) \Leftrightarrow m \le \mathop {\min }\limits_{x \in \left( {0;\; + \infty } \right)} g\left( x \right) \Leftrightarrow m \le - 3\)
Vậy m ≤ −3 là giá trị của tham số m cần tìm.

