Tìm tất cả các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm
Câu hỏi:
Tìm tất cả các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số y = x3 + x2 + mx – 1 nằm bên phải trục tung?
Trả lời:
y = x3 + x2 + mx – 1
⇒ y' = 3x2 + 2x + m
Đồ thị hàm số có điểm cực tiểu khi và chỉ khi phương trình y' = 0 có hai nghiệm phân biệt
∆' = 1 – 3m > 0 ⇔ m < \(\frac{1}{3}\)(1)
Khi đó, giả sử x1 và x2 là hai nghiệm của phương trình y' = 0
⇒ \[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - 2}}{3}\\{x_1}{x_2} = \frac{m}{3}\end{array} \right.\]
Bảng biến thiên
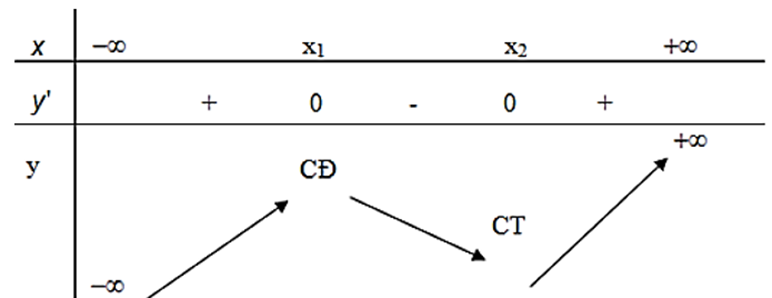
Do x1 + x2 = \(\frac{{ - 2}}{3} < 0\) nên điểm cực tiểu của đồ thị hàm số y = x3 + x2 + mx – 1 nằm bên phải trục tung
⇔ x1x2 < 0 hay \(\frac{m}{3} < 0\) tức m < 0 (2)
Từ (1) và (2) suy ra: m < 0.
