Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y= (x+1)/căn mx^2+1
Câu hỏi:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số có hai tiệm cận ngang.
Trả lời:
Nếu m = 0 thì y = x + 1 không có tiệm cận.
Nếu m < 0 thì xét dưới mẫu số ta thấy x có điều kiện ràng buộc nên không thể xét x tới vô cùng được.
Nếu m > 0 thì ta có nên sẽ có 2 tiệm cận ngang là:
Vậy m Î (0; +∞) là giá trị cần tìm.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tính giá trị lớn nhất của hàm số y = x(2 − ln x) trên đoạn [2; 3].
Xem lời giải »
Câu 2:
Tìm giá trị nhỏ nhất của hàm số y = x2ln x trên đoạn [1; 2].
Xem lời giải »
Câu 4:
Hàm số y = cos 2x nghịch biến trên khoảng nào sau đây (k Î ℤ).
Xem lời giải »
Câu 5:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Gọi H là hình chiếu của A trên SB. Tính khoảng cách giữa AH và BC.
Xem lời giải »
Câu 6:
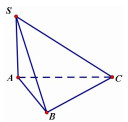
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). . Tam giác ABC vuông cân tại B và AB = a (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Xem lời giải »