Tính bán kính đường tròn ngoại tiếp hình vuông cạnh bằng 1
Câu hỏi:
Tính bán kính đường tròn ngoại tiếp hình vuông cạnh bằng 1.
Trả lời:
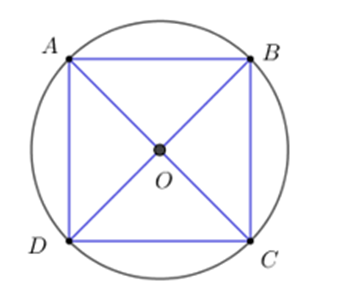
Xét hình vuông ABCD có các cạnh là 1
Tâm đường tròn ngoại tiếp hình vuông ABCD là giao điểm O của hai đường chéo AC và BD.
Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại B ta có:
AC2 = AB2 + BC2 = 1 + 1 = 2
\[ \Rightarrow AC = \sqrt 2 \]
O là trung điểm của AC nên \[OA = OC = R = \frac{1}{2}AC = \frac{{\sqrt 2 }}{2}\]
Vậy bán kính đường tròn ngoại tiếp hình vuông cạnh bằng 1 là \[\frac{{\sqrt 2 }}{2}\].


