Trên đường thẳng d lấy ba điểm A,B,C theo thứ tự đó. Trên nửa mặt phẳng bờ d
Câu hỏi:
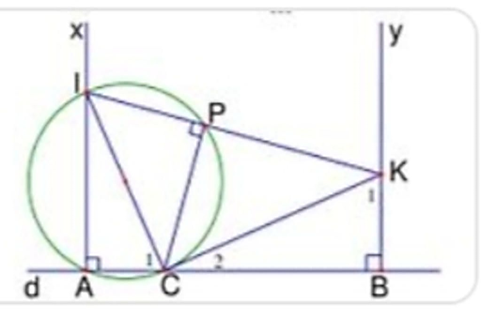
Trên đường thẳng d lấy ba điểm A,B,C theo thứ tự đó. Trên nửa mặt phẳng bờ d kẻ hai tia Ax, By cùng vuông góc với dt. Trên tia Ax lấy I. Tia vuông góc với CI tại C cắt By tại K. Đường tròn đường kính IC cắt IK tại P.
1) Chứng minh tứ giác CBPK nội tiếp được đường tròn.
2) Chứng mi nh AI.BK = AC.CB.
Trả lời:
1) Vì P thuộc đường tròn đường kính IC nên \(\widehat {CPI} = 90^\circ \)
Suy ra: \(\widehat {CPK} = 90^\circ \)
Xét tứ giác BCPK có:
\(\widehat {CPK} + \widehat {CBK} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra: BCPK nội tiếp đường tròn.
2) Vì \(\widehat {PCI} = 90^\circ \)⇒ \(\widehat {{C_1}} + \widehat {{C_2}} = 90^\circ \)
Mà \(\widehat {{K_1}} + \widehat {{K_2}} = 90^\circ \)(vì tam giác KBC vuông tại B)
Suy ra: \(\widehat {{K_1}} = \widehat {{C_1}}\)
Xét ∆IAC và ∆CBK có:
\(\widehat {{K_1}} = \widehat {{C_1}}\)
\(\widehat {IAC} = \widehat {KBC} = 90^\circ \)
⇒ ∆IAC ~ ∆CBK (g.g)
⇒ \(\frac{{AI}}{{BC}} = \frac{{AC}}{{BK}}\) ⇒ AI.BK = AC.BC

