Với giá trị nào của m, hàm số y = x^3 - 2x^2 + mx - 1 không có cực trị?

❮ Bài trước Bài sau ❯

Câu hỏi:

Với giá trị nào của m, hàm số $y = x^{3} - 2 x^{2} + m x - 1$ không có cực trị?

A. $m \geq \frac{4}{3}$

B. $m < \frac{4}{3}$

C. $m \leq \frac{4}{3}$

D. Không tồn tại

Trả lời:

Chọn A

$y' = 3 x^{2} - 4 x + m .$ Hàm số không có cực trị <=> y’=0 vô nghiệm hoặc có nghiệm kép <=> Δ' ≤ 0 <=> $2^{2} - 3 m \leq 0$ <=> $m \geq \frac{4}{3}$

Do đó hàm số không có cực trị khi $m \geq \frac{4}{3}$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số y = f(x) có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là

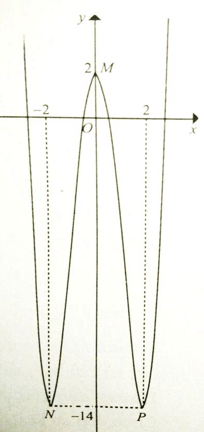
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Xem lời giải »

Câu 2:

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên

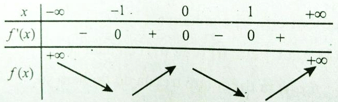
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Mệnh đề nào sau đây là đúng?

Xem lời giải »

Câu 3:

Tìm a, b, c sao cho hàm số $y = x^{3} + a x^{2} + b x + c$ có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .

Xem lời giải »

Câu 4:

Trong các mệnh đề sau, mệnh đề nào đúng?

Xem lời giải »

Câu 5:

Với giá trị nào của m, hàm số $y = - m x^{4} + 2 (m - 1) x^{2} + 1 - 2 m$ có một cực trị

Xem lời giải »

Câu 6:

Giá trị của m để hàm số $y = x^{3} - 3 m x^{2} + (m^{2} - 1) x + 2$ đạt cực đại tại x = 2 là:

Xem lời giải »

Câu 7:

Với giá trị nào của m, hàm số $y = (x - m)^{3} - 3 x$ đạt cực tiểu tại điểm có hoành độ x = 0?

Xem lời giải »

Câu 8:

Với giá trị nào của m, hàm số $y = x^{3} + 2 (m - 1) x^{2} + (m^{2} - 4 m + 1) x + 2 (m^{2} + 1)$ có hai điểm cực trị $x_{1}, x_{2}$ thỏa mãn $\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{x_{1} + x_{2}}{2}$

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Với giá trị nào của m, hàm số y = x^3 - 2x^2 + mx - 1 không có cực trị?

Xem thêm bài tập Toán có lời giải hay khác: