Cho đường thẳng d1: y = mx + 2m - 1 ( với m là tham số) và d2: y = x + 1
Câu hỏi:
Cho đường thẳng d1: y = mx + 2m – 1 ( với m là tham số) và d2: y = x + 1.
a) Với m = 2. Hãy vẽ các đường thẳng d1 và d2 trên cùng 1 mặt phẳng tọa độ . Tìm tọa độ giao điểm của 2 đường thẳng d1 và d2.
b) Tìm giá trị của m để đường thẳng d1 cắt trục hoành tại điểm có hoành độ bằng –3
c) Chứng minh rằng đường thẳng d1 luôn đi qua một điểm cố định với mọi giá trị của m.
Trả lời:
a) Với m = 2 thì ta có: d1: y = 2x + 3; d2: y = x + 1
Vẽ đường thằng đi qua 2 điểm A(0;3) và B\(\left( {\frac{{ - 3}}{2};0} \right)\) ta được d1
Vẽ đường thẳng đi qua 2 điểm C(0;1) và D(–1; 0) ta được d2
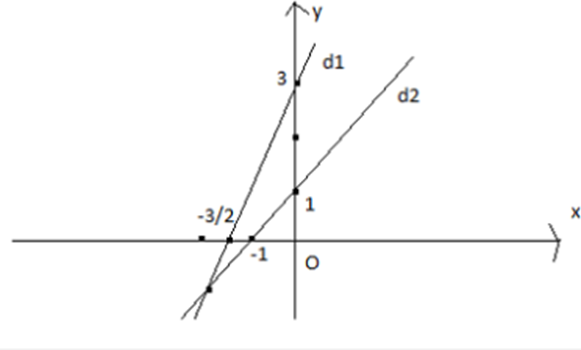
Xét phương trình hoành độ giao điểm ta có:
2x + 3 = x + 1
⇔ x = – 2
Suy ra: y = –1
Vậy 2 đường thẳng cắt nhau tại E(–2; –1).
b) d1 cắt trục hoành tại điểm có hoành độ bằng –3 tức là cắt tại điểm P(–3 ;0)
Khi đó ta có: 0 = –3m + 2m – 1
⇔ m = – 1
c) Gọi điểm cố định mà d1 luôn đi qua là M(x0; y0)
Ta có: y0 = mx0 + 2m – 1 = m(x0 + 2) – 1
⇔ m(x0 + 2) = 1 + y0
Để phương trình đúng với mọi m thì:
\(\left\{ \begin{array}{l}{x_0} + 2 = 0\\{y_0} + 1 = 0\end{array} \right.\) ⇔ \(\left\{ \begin{array}{l}{x_0} = - 2\\{y_0} = - 1\end{array} \right.\)
Vậy d1 luôn đi qua điểm cố định là M(–2;–1).

