Cho đường tròn tâm O đường kính AB. Gọi H là trung điểm của OB, MN là dây
Câu hỏi:
Cho đường tròn tâm O đường kính AB. Gọi H là trung điểm của OB, MN là dây cung bất kì qua H. Vẽ dây AA' vuông góc với MN. Lấy I là trung điểm của MN, BI cắt AA' tại D. Chứng minh:
a) Tứ giác DMNB là hình bình hành.
b) D là trung điểm của AA'.
Trả lời:
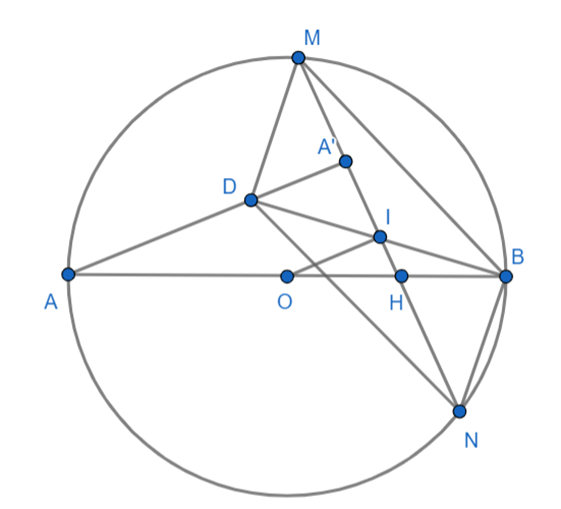
a) Nối OI ta có:
+ Xét tam giác OMN có
OM = ON (bán kính đường tròn)
⇒ Tam giác OMN cân (tam giác có hai cạnh bên bằng nhau là tam gíac cân)
MI = NI (đề bài)
⇒ OI là trung tuyến thuộc cạnh MN
⇒ OI vuông góc MN (trong tam giác cân trung tuyến thuộc cạnh đáy đồng thời là đường cao của tam giác cân)
Ta có: AA' vuông góc MN
OI vuông góc MN (cmt)
⇒ OI // AA'
Xét tam giác ABD có:
OA = OB (bán kính đường tròn)
OI // AD (chứng minh trên OI//AA')
⇒ BI = DI (đường thẳng // cạnh đáy và đi qua trung điểm của 1 cạnh bên thì cũng đi qua trung điểm của cạnh bên còn lại)
Mà MI = NI
⇒ DMNB là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành)
b) Xét tam giác OBD có
HO = HB (đề bài)
BI = DI (chứng minh trên)
⇒ HI là đường trung bình của tam giác OBD.
⇒ HI // OD
Mà HI vuông góc AA'
⇒ OD vuông góc AA'
⇒ AD = A'D (Bán kính vuông góc với dây cung thì chia đôi dây cung tại điểm cắt nhau).

