Cho hai hàm số f(x) =ax^3+bx^2+cx-1/2 và g (x) = dx^2 + ex + 1

Câu hỏi:

Cho hai hàm số $f (x) = a x^{3} + b x^{2} + c x - \frac{1}{2}$ và g (x) = dx² + ex + 1 (a, b, c, d, e Î ℝ). Biết rằng đồ thị hàm số y = f (x) và y = g (x) cắt nhau tại ba điểm có hoành độ lần lượt là −3; −1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

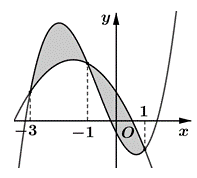
Media VietJack

Trả lời:

Phương trình hoành độ giao điểm của đồ thị f (x) và g (x) là:

$a x^{3} + b x^{2} + c x - \frac{1}{2} = d x^{2} + e x + 1$

$\Leftrightarrow a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2} = 0 (*)$

Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình (*) có ba nghiệm là −3; −1; 1.

Ta được $a (x + 3) (x + 1) (x - 1) = a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2}$

$\Leftrightarrow a (x + 3) (x^{2} - 1) = a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2}$

$\Leftrightarrow a x^{3} + 3 a x^{2} - a x - 3 a = a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2}$

Đồng nhất hai vế ta suy ra:

$\{\begin{cases} 3 a = b - d \\ - a = c - e \\ - 3 a = - \frac{3}{2} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ b - d = \frac{3}{2} \\ c - e = - \frac{1}{2} \end{cases}$

Vậy diện tích hình phẳng cần tìm là

$S = \int_{- 3}^{- 1} (\frac{1}{2} x^{3} + \frac{3}{2} x^{2} - \frac{1}{2} x - \frac{3}{2}) d x + \int_{- 1}^{1} (- \frac{1}{2} x^{3} - \frac{3}{2} x^{2} + \frac{1}{2} x + \frac{3}{2}) d x$

$= {(\frac{x^{4}}{8} + \frac{x^{3}}{2} - \frac{x^{2}}{4} - \frac{3 x}{2})|}_{- 3}^{- 1} + {(- \frac{x^{4}}{8} - \frac{x^{3}}{2} + \frac{x^{2}}{4} + \frac{3 x}{2})|}_{- 1}^{1}$

$= \frac{{(- 1)}^{4}}{8} + \frac{{(- 1)}^{3}}{2} - \frac{{(- 1)}^{2}}{4} - \frac{3 . (- 1)}{2} - \frac{{(- 3)}^{4}}{8} - \frac{{(- 3)}^{3}}{2} + \frac{{(- 3)}^{2}}{4} + \frac{3 . (- 3)}{2}$

$- \frac{1^{4}}{8} - \frac{1^{3}}{2} + \frac{1^{2}}{4} + \frac{3 . 1}{2} + \frac{{(- 1)}^{4}}{8} + \frac{{(- 1)}^{3}}{2} - \frac{{(- 1)}^{2}}{4} - \frac{3 . (- 1)}{2}$

$= \frac{1}{8} - \frac{1}{2} - \frac{1}{4} + \frac{3}{2} - \frac{81}{8} + \frac{27}{2} + \frac{9}{4} - \frac{9}{2} - \frac{1}{8} - \frac{1}{2} + \frac{1}{4} + \frac{3}{2} + \frac{1}{8} - \frac{1}{2} - \frac{1}{4} + \frac{3}{2}$ = 4.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tính giá trị lớn nhất của hàm số y = x(2 − ln x) trên đoạn [2; 3].

Xem lời giải »

Câu 2:

Tìm giá trị nhỏ nhất của hàm số y = x²ln x trên đoạn [1; 2].

Xem lời giải »

Câu 3:

Hàm số y = cos 2x đồng biến trên khoảng nào?

Xem lời giải »

Câu 4:

Hàm số y = cos 2x nghịch biến trên khoảng nào sau đây (k Î ℤ).

Xem lời giải »

Câu 5:

Cho tam giác ABC. Hãy xác định các điểm I, J, K, L thoả các đẳng thức sau:

a) $2 \vec{I B} + 3 \vec{I C} = \vec{0}$

b) $2 \vec{J A} + \vec{J C} - \vec{J B} = \vec{C A}$

c) $\vec{K A} + \vec{K B} + \vec{K C} = 2 \vec{B C}$

d) $3 \vec{L A} + 2 \vec{L C} - \vec{L B} = \vec{0}$

Xem lời giải »

Câu 6:

Cho ∆ABC. Hãy xác định các điểm I, J, K, L thoả các đẳng thức sau:

a) $2 \vec{I A} - 3 \vec{I B} = 3 \vec{B C}$

b) $\vec{J A} + \vec{J B} + 2 \vec{J C} = \vec{0}$

c) $\vec{K A} + \vec{K B} - \vec{K C} = \vec{B C}$

d) $\vec{L A} - 2 \vec{L C} = \vec{A B} - 2 \vec{A C}$

Xem lời giải »

Câu 7:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD (tham khảo hình vẽ bên). Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CMN.

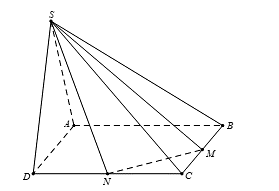
Media VietJack

Xem lời giải »

Câu 8:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách d giữa hai đường thẳng SA và BD.

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hai hàm số f(x) =ax^3+bx^2+cx-1/2 và g (x) = dx^2 + ex + 1

Xem thêm bài tập Toán có lời giải hay khác: