Cho hai hình bình hành ABCD và AB′C′D′ có chung đỉnh A. Khẳng định nào đúng
Câu hỏi:
Cho hai hình bình hành ABCD và AB′C′D′ có chung đỉnh A. Khẳng định nào đúng?
A. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {AC} \].
B. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow 0 \].
C. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {BC} \].
D. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {BD} \].
Trả lời:
Đáp án đúng là: B
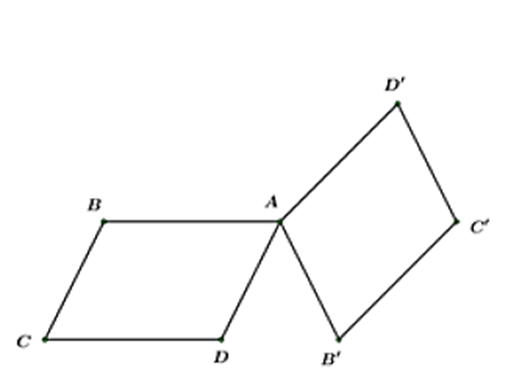
Theo quy tắc trừ và quy tắc hình bình hành ta có:
\[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \left( {\overrightarrow {AB} - \overrightarrow {AB'} } \right) + \left( {\overrightarrow {AC'} - \overrightarrow {AC} } \right) + \left( {\overrightarrow {AD} - \overrightarrow {AD'} } \right)\]
\[ = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) - \overrightarrow {AC} - \left( {\overrightarrow {AB'} + \overrightarrow {AD} } \right) + \overrightarrow {AC'} = \overrightarrow 0 \].