Cho hàm số y = ax^3 + bx^2 + cx + d có đồ thị hàm số như hình vẽ dưới đây. Khẳng định
Câu hỏi:
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào dưới đây là đúng?
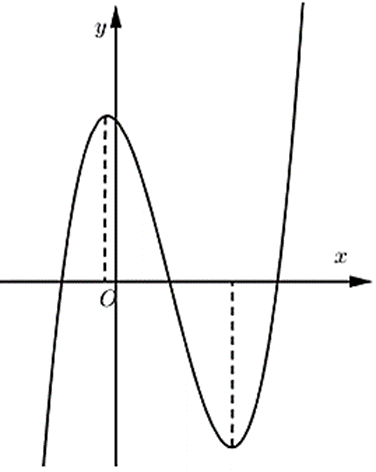
A. a < 0, b < 0, c < 0, d > 0;
B. a > 0, b < 0, c > 0, d > 0;
C. a > 0, b > 0, c < 0, d > 0;
D. a > 0, b < 0, c < 0, d > 0.
Trả lời:
Ta thấy: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \Rightarrow a > 0\)
Đồ thị hàm số cắt trục Oy tại điểm có tung độ y0 > 0 Þ d > 0
Đồ thị hàm số có 2 điểm cực trị trái dấu nên y¢ = 3ax2 + 2bx + c = 0 có hai nghiệm trái dấu
Þ 3ac < 0 Þ c < 0 (Do a > 0)
Hoành độ điểm uốn nằm bên phải trục tung nên y¢¢ = 6ax + 2b = 0 có nghiệm dương
\( \Rightarrow x = \frac{{ - b}}{{3a}} > 0 \Leftrightarrow \frac{b}{a} < 0 \Rightarrow b < 0\;\left( {do\;a > 0} \right)\)
Vậy a > 0, b < 0, c < 0, d > 0.
Chọn đáp án D.

