Cho hàm số y = ax^4 + bx^2 + c (a > 0) có ba cực trị. Nếu yCD < 0 thì đồ thị
Câu hỏi:
Cho hàm số có ba cực trị. Nếu thì đồ thị hàm số:
A. Cắt trục hoành tại 3 điểm phân biệt
B. Cắt trục hoành tại 2 điểm phân biệt
C. Nằm hoàn toàn phía trên trục hoành
D. Nằm hoàn toàn phía dưới trục hoành
Trả lời:
Đáp án C
Đồ thị hàm số bậc bốn trùng phương có ba cực trị và hệ số a > 0 có dạng:
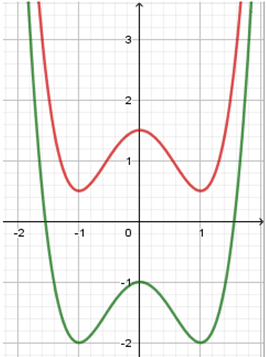
Quan sát đồ thị ta thấy nếu thì đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
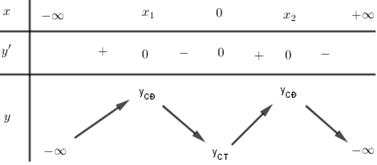
Xem lời giải »
Câu 2:
Cho hàm số có ba cực trị. Nếu thì:
Xem lời giải »
Câu 3:
Cho hàm số có ba cực trị. Nếu thì:
Xem lời giải »
Câu 4:
Hàm số có 1 cực trị nếu và chỉ nếu:
Xem lời giải »
Câu 5:
Cho hàm số có 1 cực trị. Khi đó, nếu đồ thị hàm số nằm hoàn toàn phía dưới trục hoành thì:
Xem lời giải »
Câu 6:
Cho hàm số có a < 0, b > 0. Chọn kết luận sai:
Xem lời giải »
Câu 7:
Cho hàm số có a < 0, b = 0, c > 0. Chọn kết luận sai:
Xem lời giải »
Câu 8:
Cho hàm số có a > 0, b < 0. Đồ thị hàm số có 4 điểm chung với trục hoành nếu:
Xem lời giải »

