Cho hàm số y = x^3 - 6mx + 4 có đồ thị (Cm). Gọi m0 là giá trị của m để

Câu hỏi:

Cho hàm số $y = x^{3} - 6 m x + 4$ có đồ thị (C_m). Gọi $m_{0}$ là giá trị của m để đường thẳng đi qua điểm cực đại, điểm cực tiểu của (C_m) cắt đường tròn tâm I(1;0); bán kính $\sqrt{2}$ tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích lớn nhất. Chọn khẳng định đúng?

A. $m_{0} \in (3; 4)$

B. $m_{0} \in (1; 2)$

C. $m_{0} \in (0; 1)$

D. $m_{0} \in (2; 3)$

Trả lời:

Đáp án C

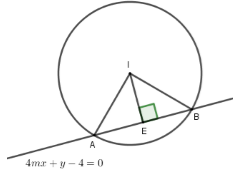
Ta có: $y' = 3 x^{2} - 6 m \Rightarrow y = y' . (\frac{1}{3} x) - 4 m x + 4$

Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là:

$y = - 4 m x + 4 \Leftrightarrow 4 m x + y - 4 = 0$

Diện tích tam giác IAB là:

$S_{I A B} = \frac{1}{2} I A . I B . \sin \hat{A I B} = \frac{1}{2} . \sqrt{2} . \sqrt{2} . \sin \hat{A I B} = \sin \hat{A I B} \leq 1$

$\Leftrightarrow S_{I A B}$ đạt giá trị lớn nhất khi $\sin \hat{A I B} = 1 \Leftrightarrow I A ⊥ I B$ hay tam giác IAB vuông cân tại I và $I A = I B = \sqrt{2}$

$\Rightarrow A B = 2 \Rightarrow d (I, A B) = \frac{1}{2} A B = 1 \Rightarrow \frac{|4 m .1 + 0 - 4|}{\sqrt{{(4 m)}^{2} + 1^{2}}} = 1 \Leftrightarrow |4 m - 4| = \sqrt{{(4 m)}^{2} + 1^{2}} \Leftrightarrow 16 m^{2} - 32 m + 16 = 16 m^{2} + 1 \Leftrightarrow m = \frac{15}{32} \in (0; 1)$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Hàm số $y = m x^{4} + (m + 3) x^{2} + 2 m - 1$ chỉ có cực đại mà không có cực tiểu khi

Xem lời giải »

Câu 2:

Tìm tất cả các giá trị của m để hàm số $y = - \frac{1}{3} x^{3} + \frac{m x^{2}}{3} + 4$ đạt giá trị cực đại tại x = 2?

Xem lời giải »

Câu 3:

Tìm tất cả các giá trị của tham số m để hàm số $y = x^{3} - 2 m x^{2} + m^{2} x + 2$ đạt giá trị cực tiểu tại x = 1

Xem lời giải »

Câu 4:

Tìm tất cả các giá trị thực của m để hàm số $y = 4 x^{3} + m x^{2} - 12 x$ đạt cực tiểu tại điểm x = - 2

Xem lời giải »

Câu 5:

Tìm tất cả các giá trị của m để đồ thị hàm số $y = x^{3} - 3 m x^{2} + 2$ có hai điểm cực trị A, B sao cho A, B và $M (1; - 2)$ thẳng hàng.

Xem lời giải »

Câu 6:

Gọi $m_{0}$ là giá trị của m thỏa mãn đồ thị hàm số $y = \frac{x^{2} + m x - 5}{x^{2} + 1}$ có hai điểm cực trị A, B sao cho đường thẳng AB đi qua điểm $I (1; - 3)$ . Khẳng định nào sau đây đúng?

Xem lời giải »

Câu 7:

Hàm số $f (x) = |\frac{x}{x^{2} + 1} - m|$ (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?

Xem lời giải »

Câu 8:

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x^{2} + m x + 2 m}{x + 1}$ có hai điểm cực trị A, B và tam giác OAB vuông tại O. Tổng tất cả các phần tử của S là:

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số y = x^3 - 6mx + 4 có đồ thị (Cm). Gọi m0 là giá trị của m để

Xem thêm bài tập Toán có lời giải hay khác: