Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi E, F lần
Câu hỏi:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi E, F lần lượt là trung điểm của AB, BC. Đẳng thức nào sau đây sai?
A. \(\overrightarrow {DO} = \overrightarrow {EB} - \overrightarrow {EO} \)
B. \(\overrightarrow {OC} = \overrightarrow {EB} + \overrightarrow {EO} \)
C. \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} = \vec 0\)
D. \(\overrightarrow {BE} + \overrightarrow {BF} - \overrightarrow {DO} = \vec 0\).
Trả lời:
Đáp án đúng là: D
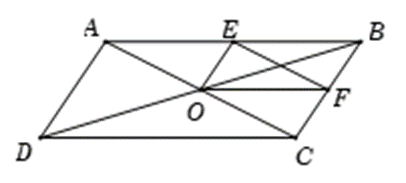
Vì ABCD là hình bình hành có O là giao điểm của hai đường chéo nên O là trung điểm của AC, BD
Xét tam giác BCD có O, F là trung điểm của BD, BC
Suy ra OF là đường trung bình
Do đó OF // CD và \(OF = \frac{1}{2}C{\rm{D}}\)
Xét tam giác BAD có O, E là trung điểm của BD, BA
Suy ra OE là đường trung bình
Do đó OE // AD và \(OE = \frac{1}{2}{\rm{AD}}\)
Ta có \(\left\{ \begin{array}{l}AB\,{\rm{//}}\,C{\rm{D}}\\OF\,{\rm{//}}\,C{\rm{D}}\end{array} \right. \Rightarrow AB\,{\rm{//}}\,{\rm{OF}}\)
\(\left\{ \begin{array}{l}AD\,{\rm{//}}\,CB\\OE\,{\rm{//}}\,A{\rm{D}}\end{array} \right. \Rightarrow CB\,{\rm{//}}\,{\rm{OE}}\)
Suy ra BEOF là hình bình hành
Do đó \(\overrightarrow {BE} + \overrightarrow {BF} = \overrightarrow {BO} \)\( \Leftrightarrow \overrightarrow {BE} + \overrightarrow {BF} - \overrightarrow {DO} = \overrightarrow {BO} - \overrightarrow {DO} = \overrightarrow {OD} - \overrightarrow {OB} = \overrightarrow {B{\rm{D}}} \)
Suy ra khẳng định D là sai
Vậy ta chọn đáp án D.

![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
