Cho hình chóp đều S.ABCD có AC = 2a, mặt bên (SBC) tạo với mặt đáy ( ABCD) một góc 45°. Tính thể tích V của khối chóp S.ABCD.
Câu hỏi:
Cho hình chóp đều S.ABCD có AC = 2a, mặt bên (SBC) tạo với mặt đáy ( ABCD) một góc 45°. Tính thể tích V của khối chóp S.ABCD.
Trả lời:
Lời giải
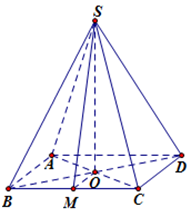
Gọi M là trung điểm của BC, O là giao điểm của AC và BD
Ta có: \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right)\)
\( \Rightarrow \left( {\widehat {\left( {SBC} \right),\;\left( {ABCD} \right)}} \right) = \left( {\widehat {SM,\;OM}} \right) = \widehat {SMO} = 45^\circ \)
Do \(AC = 2a \Rightarrow AB = a\sqrt 2 \)
\( \Rightarrow OM = \frac{{a\sqrt 2 }}{2} \Rightarrow SO = OM = \frac{{a\sqrt 2 }}{2}\).
Ta có: SABCD = 2a2
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO\,.\,{S_{ABCD}} = \frac{1}{3}\,.\,\frac{{a\sqrt 2 }}{2}\,.\,2{a^2} = \frac{{{a^3}\sqrt 2 }}{3}\).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho \(\left\{ \begin{array}{l}a + b \ne 0\\a;\;b \ne 0\end{array} \right.\). Chứng minh rằng: \[\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{{\left( {a + b} \right)}^2}}}} = \left| {\frac{1}{a} + \frac{1}{b} - \frac{1}{{a + b}}} \right|\].
Xem lời giải »
Câu 2:
Cho a, b, c là các số hữu tỉ khác 0 thỏa mãn a + b + c = 0. Chứng minh rằng: \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\) là bình phương của một số hữu tỉ.
Xem lời giải »
Câu 3:
Cho biểu thức: \[A = \sqrt {\frac{{{{\left( {{x^2} - 3} \right)}^2} + 12{x^2}}}{{{x^2}}}} + \sqrt {{{\left( {x + 2} \right)}^2} - 8x} \].
a) Rút gọn A.
b) Tìm các giá trị nguyên của x để giá trị của A là một số nguyên.
Xem lời giải »
Câu 4:
Cho biểu thức: \(P = \left( { - \frac{2}{3}{x^2}{y^3}{z^2}} \right){\left( { - \frac{1}{2}xy} \right)^3}{\left( {x{y^2}z} \right)^2}\).
a) Rút gọn biểu thức P.
b) Tìm bậc và hệ số biểu thức B.
c) Tìm giá trị các biến để P £ 0.
Xem lời giải »
Câu 5:
Cho mặt phẳng (P) và hai đường thẳng song song a và b. Khẳng định nào sau đây đúng?
Xem lời giải »
Câu 6:
Cho một mặt phẳng (P) và hai đường thẳng song song a, b. Mệnh đề nào sau đây là sai?
Xem lời giải »
Câu 7:
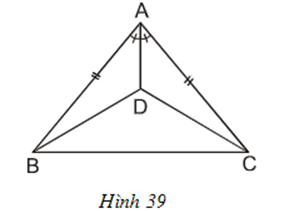
Cho hình 39.
a) Chứng minh ΔABD = ΔACD.
b) So sánh góc DBC và góc DCB.
Xem lời giải »
Câu 8:
Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh DABD = DACD.
b) Chứng minh rằng AM = 2.BD.
c) Tính số đo \[\widehat {MAD}\].
Xem lời giải »



