Cho hình chóp S.ABC có SA = SB = SC = a căn bậc hai 3, AB = AC = 2a
Câu hỏi:
Cho hình chóp S.ABC có SA = SB = SC = \(a\sqrt 3 ,\) AB = AC = 2a, BC = 3a. Thể tích của khối chóp S.ABC bằng
A. \(\frac{{\sqrt 5 {a^3}}}{2}.\)
B. \(\frac{{\sqrt {35} {a^3}}}{2}.\)
C. \(\frac{{\sqrt {35} {a^3}}}{6}.\)
D. \(\frac{{\sqrt 5 {a^3}}}{4}.\)
Trả lời:
Đáp án đúng là: D
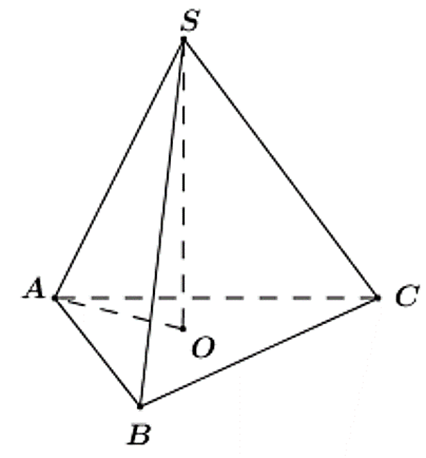
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì SA = SB = SC (gt) nên SO ⊥ (ABC).
Gọi p là nửa chu vi tam giác ABC ta có \(p = \frac{{AB + BC + CA}}{2} = \frac{{7a}}{2}.\)
⇒ \({S_{ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - CA} \right)} = \frac{{3\sqrt 7 {a^2}}}{4}.\)
OA là bán kính đường tròn ngoại tiếp ∆ABC nên
\(OA = \frac{{AB\,.\,BC\,.\,CA}}{{4{S_{ABC}}}} = \frac{{2a\,.\,3a\,.\,2a}}{{4.\frac{{3\sqrt 7 {a^2}}}{4}}} = \frac{{4a\sqrt 7 }}{7}.\)
Vì SO ⊥ (ABC) nên SO ⊥ OA, do đó tam giác SOA vuông tại O.
Áp dụng định lí Py-ta-go trong tam giác vuông SOA, ta có:
\(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {3{a^2} - \frac{{16{a^2}}}{7}} = \frac{{a\sqrt {35} }}{7}.\)
Vậy \[{V_{S.ABC}} = \frac{1}{3}\,.\,SO\,.\,{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt {35} }}{7} \cdot \frac{{3\sqrt 7 {a^2}}}{4} = \frac{{{a^3}\sqrt 5 }}{4}.\]

