Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc (ABCD)
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA ⊥ (ABCD), \[SA = a\sqrt 3 \]. Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM.
Trả lời:
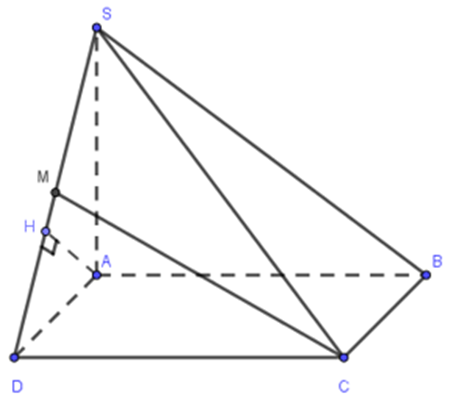
AB // CD Þ AB // (SCD) ⊃ CM
Þ d(AB,CM) = d(AB;(SCD)) = d(A,(SCD))
Kẻ AH ⊥ SD, H ∈ SD (1) ta có:
CD ⊥ AD, CD ⊥ SA Þ CD ⊥ (SAD) Þ SD ⊥ AH (2)
Từ (1),(2) suy ra: d(A; (SCD)) = AH
Þ d(AB,CM) = AH
Tam giác SAD vuông tại A, AH ⊥ SD, H ∈ SD, suy ra:
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}}\]
\[A{H^2} = \frac{{3{a^2}}}{4} \Rightarrow AH = \frac{{a\sqrt 3 }}{2}\]
Vậy khoảng cách giữa 2 đường thẳng CM và AB là \[\frac{{a\sqrt 3 }}{2}\].


