Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Gọi I, J lần lượt là trung
Câu hỏi:
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA′ và BB′. Tính thể tích của khối đa diện ABCIJC′.
Trả lời:
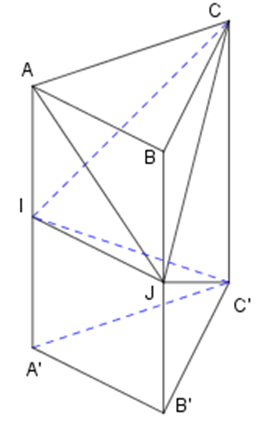
Vì I, J là trung điểm của AA′, BB′ nên VABCIJ = VA′B′C′IJ = 2VAIJC.
Vì SΔICC′ = 2SΔAIC Þ VJICC′ = 2VJAIC
Mà VABCA′B′C′ = VABCIJ + VA′B′C′IJ + VJICC′
\[ \Rightarrow {V_{ABCIJ}} = \frac{1}{3}V\]
\[ \Rightarrow {V_{ABCIJC'}} = \frac{2}{3}V\]
Vậy thể tích của khối đa diện ABCIJC′ là \[\frac{2}{3}V\].


