Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Góc
Câu hỏi:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Góc giữa CA’ và mặt (AA’B’B) bằng 30o. Tính thể tích khối lăng trụ ABC.A’B’C’.
Trả lời:
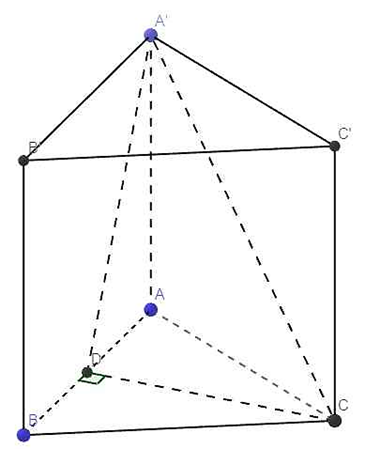
Gọi D là trung điểm AB Þ CD ⊥ AB
Þ CD ⊥ (AA′B′B)
\[ \Rightarrow \widehat {CA'D} = 30^\circ \]
\[CD = \frac{{a\sqrt 3 }}{2} \Rightarrow A'D = \frac{{CD}}{{\tan 30^\circ }} = \frac{{3a}}{2}\]
\[ \Rightarrow A'A = \sqrt {C{D^2} - A{D^2}} = a\sqrt 2 \]
\[V = \frac{1}{3}A'A.{S_{ABC}} = \frac{1}{3}.a\sqrt 2 .\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 6 }}{{12}}\]
Vậy thể tích khối lăng trụ ABC.A’B’C’ là \[\frac{{{a^3}\sqrt 6 }}{{12}}\].


