Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a. Gọi M, N lần lượt là trung
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích khối chóp A.BCNM. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC).
A. \(\frac{{{a^3}\sqrt 5 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 5 }}{4}\)
C. \(\frac{{{a^3}\sqrt 5 }}{2}\)
D. \(\frac{{{a^3}\sqrt 5 }}{6}\)
Trả lời:
Đáp án đúng là: B
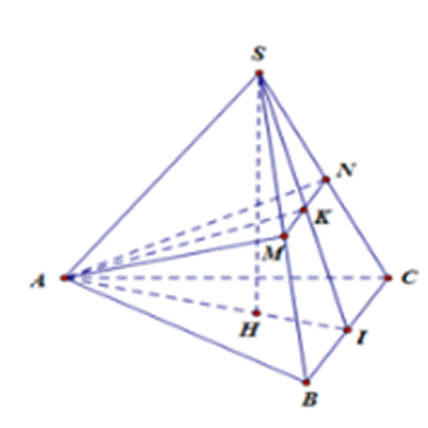
Gọi I là trung điểm của BC thì \(AI \bot BC\)
Gọi K là trung điếm của MN thì \(AK \bot MN\)
Mặt khác \((AMN) \bot (SBC)\) nên \(AK \bot (SBC) \Rightarrow AK \bot SI\)
Suy ra tam giác SAI cân tại A do đó SA = AI
Vì tam giác ABC đều cạnh 2a có AI là đường cao, trung tuyến nên \(AI = a\sqrt 3 \)
Suy ra \(SA = a\sqrt 3 \)
Gọi H là trực tâm tam giác ABC thì \(AH = \frac{2}{3}AI = \frac{{2a\sqrt 3 }}{3}\)
Khi đó tam giác SAH vuông tại H
Suy ra \(SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{3}\)
Ta có: \({S_{ABC}} = \frac{1}{2}AI.BC = \frac{1}{2}.a\sqrt 3 .2{\rm{a}} = {a^2}\sqrt 3 \)
Thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \frac{1}{3}.SH.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt {15} }}{3}.{a^2}\sqrt 3 = \frac{{{a^3}\sqrt 5 }}{3}\)
Vì \({V_{S.ANC}} = \frac{1}{4}{V_{S.ABC}} \Rightarrow {V_{A.BCMM}} = \frac{3}{4}{V_{SABC}} = \frac{{{a^3}\sqrt 5 }}{4}\)
Vậy ta chọn đáp án B.


