Cho hình nón có bán kính đáy là 5a, độ dài đường sinh là 13a. Thể tích khối cầu nội
Câu hỏi:
Cho hình nón có bán kính đáy là 5a, độ dài đường sinh là 13a. Thể tích khối cầu nội tiếp hình nón bằng:
A. \(\frac{{4000\pi {a^3}}}{{81}}\)
B. \(\frac{{4000\pi {a^3}}}{{27}}\)
C. \(\frac{{40\pi {a^3}}}{9}\)
D. \(\frac{{400\pi {a^3}}}{{27}}\).
Trả lời:
Đáp án đúng là: A
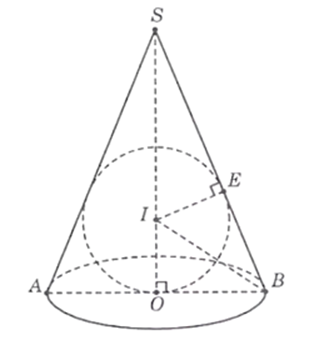
Xét mặt phẳng qua trục SO của hình nón ta được thiết diện là tam giác cân SAB.
Mặt phẳng đó cắt mặt cầu theo đường tròn có bán kính r (bán kính mặt cầu) và nội tiếp trong tam giác cân SAB.
Trong tam giác vuông SOB, gọi I là giao điểm của đường phân giác trong góc B với đường thẳng SO.
Chứng minh được I là tâm đường tròn nội tiếp tam giác và bán kính r = IO = IE (E là hình chiếu vuông góc của I trên SB).
Theo tính chất phân giác, ta có \(\frac{{IS}}{{IO}} = \frac{{BS}}{{BO}} = \frac{{13}}{5}\).
Lại có \(IS + IO = SO = \sqrt {S{B^2} - O{B^2}} = 12\).
Từ đó suy ra \(IS = \frac{{26}}{3},IO = \frac{{10}}{3}\).
Ta có \(\Delta SEI\Delta SOB\) nên
\(\frac{{IE}}{{IS}} = \frac{{BO}}{{BS}} = \frac{5}{{13}} \Rightarrow IE = \frac{5}{{13}}IS = \frac{{10}}{3}.\)
Thể tích khối cầu:
\(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {\left( {\frac{{10a}}{3}} \right)^3} = \frac{{4000\pi {a^3}}}{{81}}({\rm{dvtt}})\)
Vậy ta chọn đáp án A.


