Cho hình nón đỉnh S, góc ở đỉnh bằng 120°, đáy là hình tròn (O; 3R). Cắt hình
Câu hỏi:
Cho hình nón đỉnh S, góc ở đỉnh bằng 120°, đáy là hình tròn (O; 3R). Cắt hình nón bởi mặt phẳng qua S và tạo với đáy góc 60°. Diện tích thiết diện là:
A. \(2\sqrt 2 {R^2}\)
B. \(4\sqrt 2 {R^2}\)
C. \(6\sqrt 2 {R^2}\)
D. \(8\sqrt 2 {R^2}\).
Trả lời:
Đáp án đúng là: B
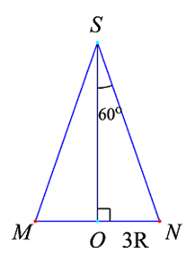
Thiết diện qua trục là tam giác SMN \( \Rightarrow \widehat {MSN} = 120^\circ \Rightarrow \widehat {OSN} = 60^\circ \)
Ta có: \(SO = \frac{{ON}}{{\tan 60^\circ }} = \frac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)
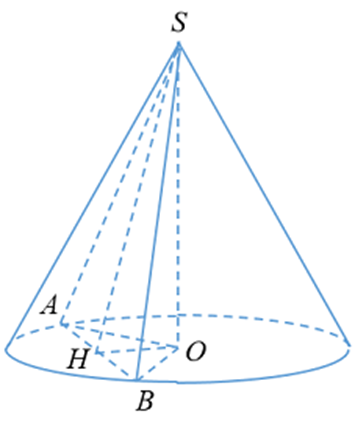
Vì (SAB) tạo với đáy góc 60°\( \Rightarrow \widehat {SHO} = 60^\circ \)
Ta có: \(OH = \frac{{SO}}{{\tan 60^\circ }} = \frac{{R\sqrt 3 }}{{\sqrt 3 }} = R\)
Vì tam giác SOH vuông tại O nên
\({\rm{S}}{O^2} + O{H^2} = S{H^2} \Leftrightarrow {(R\sqrt 3 )^2} + {R^2} = S{H^2} \Leftrightarrow SH = 2R\)
Vì tam giác BOH vuông tại H nên
\(O{H^2} + H{B^2} = O{B^2} \Leftrightarrow H{B^2} = {(3R)^2} - {R^2} \Leftrightarrow HB = 2R\sqrt 2 \)
\( \Rightarrow AB = 2HB = 4R\sqrt 2 \)
Ta có: \({S_{SAB}} = \frac{1}{2}.SH.AB = \frac{1}{2}.2R.4R\sqrt 2 = 4\sqrt 2 .{R^2}\)
Vậy ta chọn đáp án B.

![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
