Cho hình thang cân ABCD có đáy lớn CD = 3, đáy nhỏ AB = 1 và AD = BC = căn bậc hai 5
Câu hỏi:
Cho hình thang cân ABCD có đáy lớn CD = 3, đáy nhỏ AB = 1 và AD = BC = \(\sqrt 5 \), gọi I là giao điểm của hai đường chéo hình thang, gọi H là trực tâm của tam giác BDC. Phân tích vectơ \(\overrightarrow {IH} \) theo vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} \).
Trả lời:
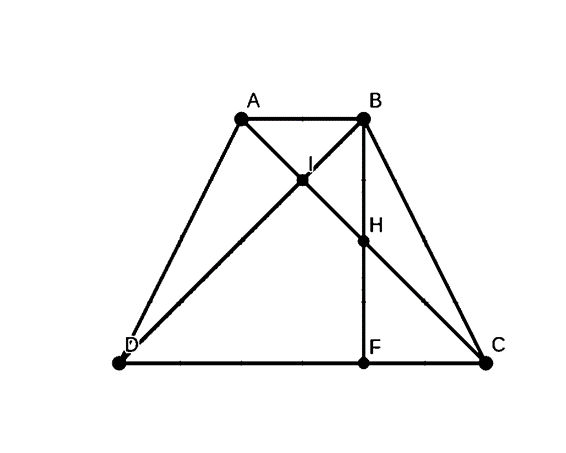
Gọi BH ∩ CD = F
Suy ra: CF = \(\frac{{CD - AB}}{2} = 1 \Rightarrow DF = 2 \Rightarrow \widehat {BDC} = 45^\circ \)
⇒ ΔIDC vuông cân tại I ⇒ CI ⊥ BD ⇒ H ∈ CI
⇒ ΔIBH vuông cân tại I
⇒ \(\overrightarrow {IH} = \overrightarrow {AI} = \frac{1}{4}\overrightarrow {AC} = \frac{1}{4}\left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) = \frac{1}{4}\left( {\overrightarrow {AD} + 3\overrightarrow {AB} } \right)\).

