Cho hình thang vuông ABCD, biết góc A = góc D = 90 độ, lấy điểm M thuộc cạnh DC
Câu hỏi:
Cho hình thang vuông ABCD, biết \(\widehat A = \widehat D = 90^\circ \), lấy điểm M thuộc cạnh DC, ∆BMC là tam giác đều. Số đo \(\widehat {ABC}\) là:
Trả lời:
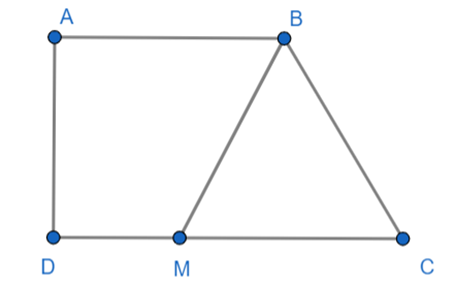
Ta có: BMC là tam giác đều nên \(\widehat {BMC} = \widehat {CBM} = \widehat {CBM} = 60^\circ \)
Suy ra: \(\widehat {DMB} = 180^\circ - 60^\circ = 120^\circ \)
Ta có: \(\widehat A + \widehat D + \widehat B + \widehat C = 360^\circ \)
Suy ra: \[\widehat {ABC} = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ \].