Cho hình vuông ABCD. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA
Câu hỏi:
Cho hình vuông ABCD. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính SMNPQ theo SABCD?
Trả lời:
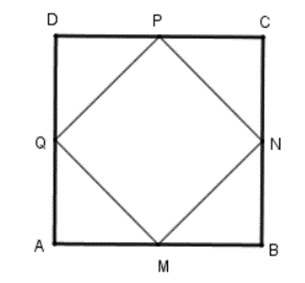
Gọi cạnh của hình vuông ABCD là a.
Vì ABCD là hình vuông là M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA nên ta có AM = MB = BN = NC = CP = PD = DQ = QA.
Từ đó: ΔAQM = ΔBMN = ΔCPN = ΔDQP (c.g.c)
SQAM = SMNB = SCPN = SDPQ = \(\frac{{{a^2}}}{8}\).
Lại có SABCD = a2.
Nên SMNPQ = SABCD – SAMQ – SMBN – SCPN – SDPQ = a2 – \(4.\frac{{{a^2}}}{8} = \frac{1}{2}\)SABCD.
Vậy SMNPQ = \(\frac{1}{2}\)SABCD.