Cho hình vuông ABCD. Trên cạnh các AD, DC lần lượt lấy các điểm E, F sao cho AE
Câu hỏi:
Cho hình vuông ABCD. Trên cạnh các AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Gọi M, N lần lượt là trung điểm của EF, BF.
a) Chứng minh các tam giác ADF và BAE bằng nhau.
b) Chứng minh MN vuông góc AF.
Trả lời:
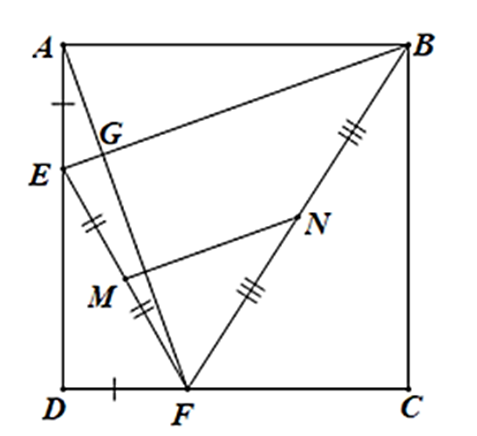
a) Vì ABCD là hình vuông nên AB = AD
Xét DADF và DBAE có
AB = AD (chứng minh trên)
\(\widehat {BAE} = \widehat {ADF} = 90^\circ \)
AE = DF (giả thiết)
Suy ra ∆ADF = ∆BAE (c.g.c).
b) Vì ∆ADF = ∆BAE nên \[\widehat {FAD} = \widehat {EBA};\widehat {AFD} = \widehat {BEA}\] (các cặp góc tương ứng)
Gọi G là giao điểm của AF và BE
Xét tam giác AGE có
\(\widehat {AGE} + \left( {\widehat {AEG} + \widehat {GAE}} \right) = 180^\circ \)(tổng ba góc trong một tam giác)
Suy ra \(\widehat {AGE} + \left( {\widehat {AFD} + \widehat {FAD}} \right) = 180^\circ \)
Hay \(\widehat {AGE} + 90^\circ = 180^\circ \)
Suy ra \(\widehat {AGE} = 90^\circ \)
Do đó BE ⊥ AF
Xét tam giác EBF có M là trung điểm của EF, N là trung điểm của BF
Suy ra MN là đường trung bình của tam giác
Do đó MN // BE
Mà BE ⊥ AF (chứng minh trên)
Suy ra MN ⊥ AF
Vậy MN ⊥ AF.

