Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, góc BAC = 120 độ
Câu hỏi:
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, \(\widehat {BAC} = 120^\circ \), biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC
A. \(\frac{{{a^3}}}{3}\)
B. \(\frac{{{a^3}}}{9}\)
C. \[{{\rm{a}}^3}\sqrt 2 \]
D. \(\frac{{{a^3}}}{2}\).
Trả lời:
Đáp án đúng là: B
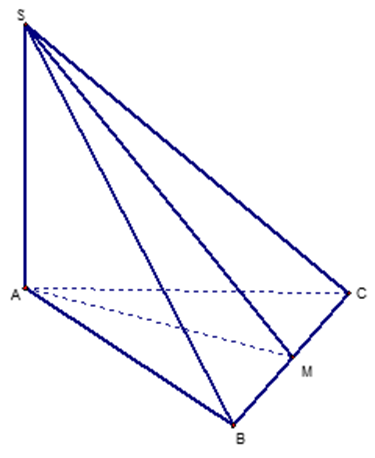
Gọi M là trung điểm của BC. Vì ∆ABC cân tại A nên AM ⊥ BC và AM là phân giác của \(\widehat {BAC}\)
Suy ra \(\widehat {BAM} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.120^\circ = 60^\circ \)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AM \bot BC}\\{SM \bot BC}\\{(SBC) \cap (ABC) = BC}\end{array}} \right.\)
Suy ra góc giữa (SBC) và (ABC) là \(\widehat {SMA}\) nên \(\widehat {SMA} = 45^\circ \)
Xét tam giác BAM có:
\(\sin \widehat {BAM} = \frac{{BM}}{{AB}} \Rightarrow AB = \frac{{BM}}{{\sin \widehat {BAM}}} = \frac{a}{{\sin 60^\circ }} = \frac{{2{\rm{a}}}}{{\sqrt 3 }}\)
\(\tan \widehat {BAM} = \frac{{BM}}{{AM}} \Rightarrow AM = \frac{{BM}}{{\tan \widehat {BAM}}} = \frac{a}{{\tan 60^\circ }} = \frac{a}{{\sqrt 3 }}\)
Xét tam giác SAM vuông tại A có
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} \Rightarrow SA = AM.\tan \widehat {SMA} = \frac{a}{{\sqrt 3 }}.\tan 45^\circ = \frac{a}{{\sqrt 3 }}\)
Diện tích tam giác ABC là \[{{\rm{S}}_{ABC}} = \frac{1}{2}AM.BC = \frac{1}{2}.\frac{{\rm{a}}}{{\sqrt 3 }}.2{\rm{a}} = \frac{{{a^2}\sqrt 3 }}{3}\]
Tính thể tích khối chóp S.ABC là
\({V_{S.ABC}} = \frac{1}{3}.SA.{S_{ABC}} = \frac{1}{3}.\frac{a}{{\sqrt 3 }}.\frac{{{a^2}\sqrt 3 }}{3} = \frac{{{a^3}}}{9}\)
Vậy ta chọn đáp án B.


