Cho (O, R), lấy điểm A cách O một khoảng 2R. Kẻ các tiếp tuyến AB và AC với đường
Câu hỏi:
Cho (O, R), lấy điểm A cách O một khoảng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh tam giác OBA vuông tại B và tam giác OAK cân tại K.
b) Đường thẳng KI cắt AB tại M. Chứng minh KM là tiếp tuyến của đường tròn (O).
Trả lời:
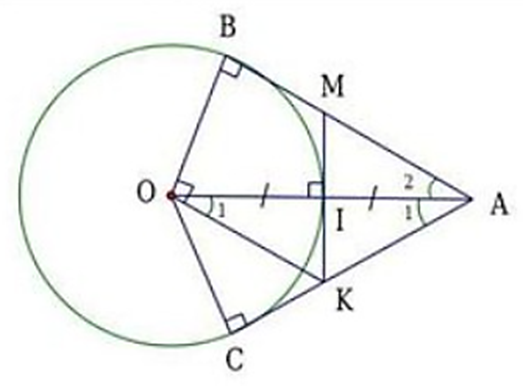
a) Xét đường tròn (O) có AB là tiếp tuyến ⇒ AB ⊥ OB ⇒ ∆OBA vuông tại B.
Ta có: AB ⊥ OB, OK ⊥ OB ⇒ AB // OK ⇒ \(\widehat {{O_1}} = \widehat {{A_2}}\) (so le trong)
Mà \(\widehat {{A_1}} = \widehat {{A_2}}\) (tính chất hai tiếp tuyến cắt nhau)
⇒ \(\widehat {{O_1}} = \widehat {{A_1}}\) ⇒ ∆OAK cân tại K.
b) Ta có: KM và đường tròn (O) có điểm I chung (1).
Mặt khác: OI = R, OA = 2R ⇒ IA = R ⇒ KI là trung tuyến của ∆OKA
Mà ∆OKA cân tại K (CMT)
⇒ KI ⊥ OA hay KM ⊥ OI (2)
Từ (1) và (2) ⇒ KM là tiếp tuyến của đường tròn (O).

