Cho tam giác ABC, gọi M và N lần lượt là trung điểm của AB và AC. Trên tia
Câu hỏi:
Cho tam giác ABC, gọi M và N lần lượt là trung điểm của AB và AC. Trên tia đối của tia NM lấy điểm D sao cho ND = NM.
a) Chứng minh: AD // MC.
b) Chứng minh: BC = 2MN.
Trả lời:
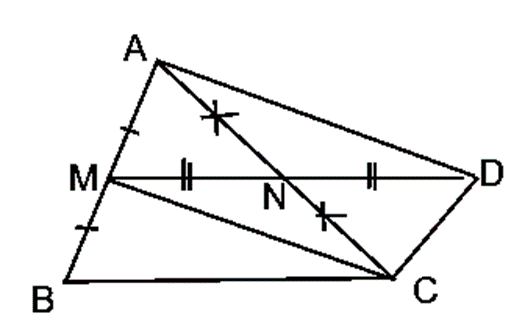
a) Tứ giác AMCD có 2 đường chéo cắt nhau tại trung điểm mỗi đường ⇒ AMCD là hình bình hành
⇒ AD // MC.
b) Theo câu a) tứ giác AMCD là hình bình hành ⇒ CD // AM và CD = AM.
Mà AM = MB và đường thẳng AM cũng là đường thẳng MB
⇒ CD song song và bằng MB
⇒ MBCD là hình bình hành vì có 2 cạnh đối song song và bằng nhau
⇒ BC = MD
Mà MD = 2 MN ⇒ BC = 2MN.

