Câu hỏi:
Cho tam giác ABC vuông tại A, AC = b, AB = c. Lấy điểm M trên cạnh BC sao cho \(\widehat {BAM} = 30^\circ \).Tính tỉ số \(\frac{{MB}}{{MC}}\).
Trả lời:
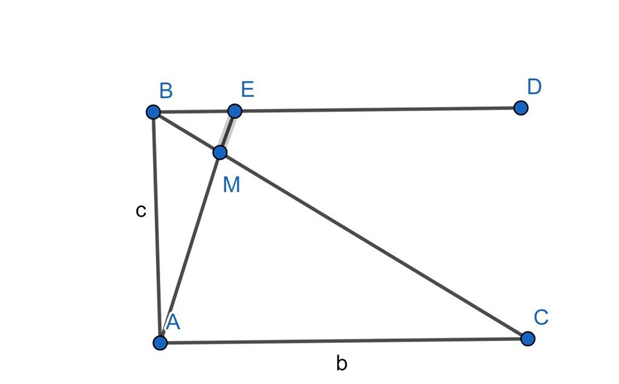
Kẻ BD// AC, AM cắt BD tại E.
Xét ΔEAB có:
EB = AB . tan30° = \(\frac{{c\sqrt 3 }}{3}\)
Do BD // AC hay BE // AC nên \(\frac{{EB}}{{CA}} = \frac{{BM}}{{MC}} = \frac{{c\sqrt 3 }}{3}:b = \frac{{c\sqrt 3 }}{{3b}}\)
Câu 1:
Tính tích phân\(\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\sqrt {1 + \sin x} dx} \).
Câu 3:
Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right|;\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right|\).
Câu 4:
Cho tam giác đều cạnh a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|;\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Câu 5:
Trong mặt phẳng tọa độ Oxy,cho ΔABC biết A(2; 4), B(5; 1), C(−1; −2). Phép tịnh tiến theo vectơ \(\overrightarrow {BC} \) biến ΔABC thành ΔA'B'C' tương ứng các điểm. Tìm tọa độ trọng tâm G’ của ΔA'B'C'.
Câu 6:
Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm đi 84 m2.
Câu 7:
Tính bán kính đường tròn ngoại tiếp hình thang cân biết hình thang cân ABCD (AB song song CD) có AB = 6cm; CD = 8cm và đường cao AH = 7cm.
