Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm
Câu hỏi:
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a) Chứng minh tứ giác AEBM là hình thoi.
b) Gọi I là trung điểm của AM . Chứng minh E, I, C thẳng hàng.
c) Tam giác ABC có thêm điều kiện gì thì AEBM là hình vuông.
Trả lời:
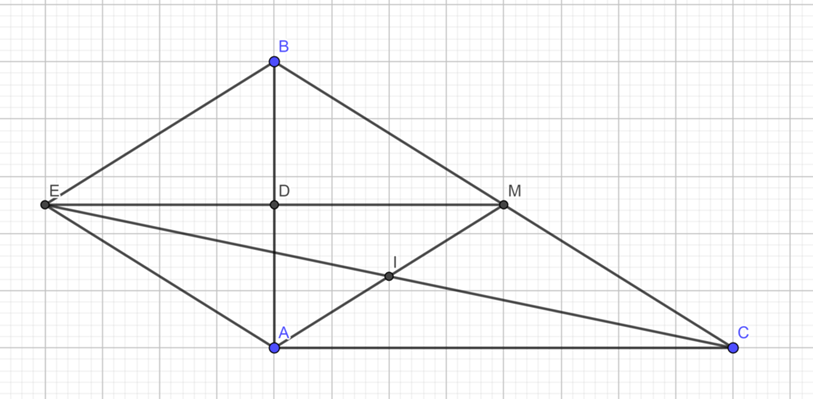
a) Xét tam giác ABC vuông tại A có:
M là trung điểm của BC
⇒ AM = MB = MC = \(\frac{{BC}}{2}\)
Xét tứ giác AEBM có:
D là trung điểm của AB
D là trung điểm cuả ME
⇒ Tứ giác AEBM là hình bình hành
Mặt khác MA = MB
⇒ Tứ giác AEBM là hình thoi
b) Ta có tứ giác AEBM là hình thoi
⇒ AE // BM và AE = BM
Mà BM = CM ⇒ AE = CM
Xét tứ giác AEMC có:
AE // CM
AE = CM
⇒ Tứ giác AEMC là hình bình hành
Có I là trung điểm của AM
⇒ I là trung điểm của EC
⇒ E; I; C thẳng hàng
c) Ta có hình thoi AEBM là hình vuông
⇔ \(\widehat {AMB} = 90^\circ \)⇔ AM ⊥ BC
⇔ Tam giác ABC vuông cân tại A.

