Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC
Câu hỏi:
Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
Trả lời:
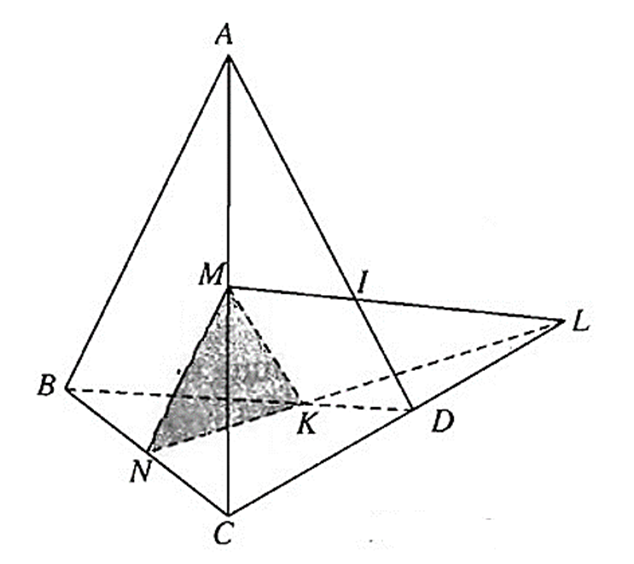
Nhận xét. Trên hình vẽ 2.23 không có sẵn đường thẳng nào của mặt phẳng (MNK) cắt AD. Ta xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến ∆ của (ACD) với (MNK). Sau đó tìm giao điểm I của ∆ và AD, I chính là giao điểm phải tìm.
Gọi L = NK ∩ CD
Ta có L ∈ NK ⇒ L ∈ (MNK)
L ∈ CD ⇒ L ∈ (ACD)
Nên ML = (ACD) ∩ (MNK) = Δ
Δ ∩ AD = I ⇒ I = (MNK) ∩ AD.

