Cho tứ giác ABCD có a là góc nhọn tạo bởi hai đường chéo. Chứng minh rằng
Câu hỏi:
Cho tứ giác ABCD có a là góc nhọn tạo bởi hai đường chéo. Chứng minh rằng \({S_{ABCD}} = \frac{1}{2}.AC.BD.\sin a\).
Trả lời:
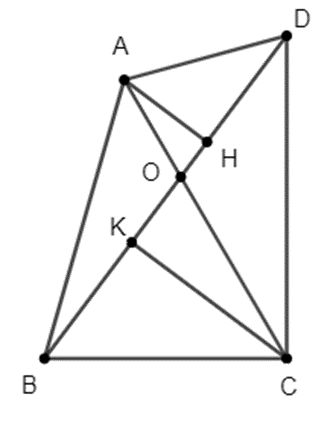
Gọi O là giao điểm hai đường chéo AC và BD và \(\widehat {AOD} = \widehat {BOC} = a < 90^\circ \)
Kẻ AH và CK vuông góc với BD. Ta có:
\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}} = \frac{1}{2}.BD.AH + \frac{1}{2}.BD.CK\)
\( = \frac{1}{2}.BD.\left( {AH + CK} \right)\) (1)
Lại có AH = OA.sina; CK = OC.sina
Do đo AH + CK = (OA + OC).sina = AC.sina (2)
Từ (1) và (2) suy ra \({S_{ABCD}} = \frac{1}{2}.AC.BD.\sin a\)