Cho x, y là các số thực thỏa mãn x + y = căn (x - 1) + căn (2y + 2). Gọi M, m

Câu hỏi:

Cho x, y là các số thực thỏa mãn $x + y = \sqrt{x - 1} + \sqrt{2 y + 2}$ . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của $P = x^{2} + y^{2} + 2 (x + 1) (y + 1) + 8 \sqrt{4 - x - y}$ . Tìm giá trị M + m

A. 41

B. 44

C. 42

D. 43

Trả lời:

Đáp án D

Đk: $x \geq 1; y \geq - 1$ . Đặt $t = x + y; t \geq 0$

Có $\sqrt{x - 1} + \sqrt{2 y + 2} = \sqrt{x - 1} + \sqrt{2} . \sqrt{y + 1} \leq \sqrt{3 (x + y)}$

$\Rightarrow x + y \leq \sqrt{3 (x + y)}$

Vậy $t \leq \sqrt{3} t \Leftrightarrow t^{2} - 3 t \leq 0 \Leftrightarrow 0 \leq t \leq 3$

$P = {(x + y)}^{2} + 2 (x + y) + 2 + 8 \sqrt{4 - (x + y)}$ nên $P = t^{2} + 2 t + 2 + 8 \sqrt{4 - t}$

$P' = 2 t + 2 - \frac{4}{\sqrt{4 - t}} P' = 0 \Leftrightarrow (2 t + 2) \sqrt{4 - t} = 4 \Leftrightarrow [\begin{matrix} t = 0 \\ t = 1 \pm 2 \sqrt{2} \notin [0; 3] \end{matrix} P (0) = 18; P (3) = 25$

Suy ra $M = 25, m = 18 \Rightarrow M + m = 43$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{4} - 2 m x^{2} + 2 m - 4$ đi qua điểm $N (- 2; 0)$

Xem lời giải »

Câu 2:

Có bao nhiêu giá trị nguyên của tham số m để đường thẳng $y = m (x - 4)$ cắt đồ thị của hàm số $y = (x^{2} - 1) (x^{2} - 9)$ tại bốn điểm phân biệt?

Xem lời giải »

Câu 3:

Hàm số $y = {(x + m)}^{3} + {(x + n)}^{3} - x^{3}$ (tham số m, n) đồng biến trên khoảng $(- \infty; + \infty)$ . Giá trị nhỏ nhất của biểu thức $P = 4 (m^{2} + n^{2}) - m - n$ bằng:

Xem lời giải »

Câu 4:

Hình vẽ bên là đồ thị của hàm số y = f(x)

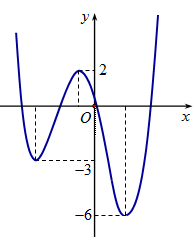
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số $y = |f (x - 1) + m|$ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:

Xem lời giải »

Câu 5:

Tìm m để hàm số $y = \frac{2 \cot x + 1}{\cot x + m}$ đồng biến trên khoảng $(\frac{π}{4}; \frac{π}{2})$ ?

Xem lời giải »

Câu 6:

Hàm số $f (x) = |8 x^{4} - 8 x^{2} + 1|$ đạt giá trị lớn nhất trên đoạn $[- 1; 1]$ tại bao nhiêu giá trị của x?

Xem lời giải »

Câu 7:

Cho x, y là những số thực thỏa mãn $x^{2} - x y + y^{2} = 1$ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P = \frac{x^{4} + y^{4} + 1}{x^{2} + y^{2} + 1}$ . Giá trị của A = M + 15m là:

Xem lời giải »

Câu 8:

Tìm tất cả những giá trị thực của m để bất phương trình sau có nghiệm với mọi x thuộc tập xác định $\sqrt[4]{2 x} + \sqrt{2 x} + 2 \sqrt[4]{6 - x} + 2 \sqrt{6 - x} > m$

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho x, y là các số thực thỏa mãn x + y = căn (x - 1) + căn (2y + 2). Gọi M, m

Xem thêm bài tập Toán có lời giải hay khác: