Hình chóp tam giác đều S.ABC có cạnh đáy là a và cạnh bên tạo với đáy một góc 45

Hình chóp tam giác đều S.ABC có cạnh đáy là a và cạnh bên tạo với đáy một góc 45°. Tính theo a thể tích khối chóp S.ABC.

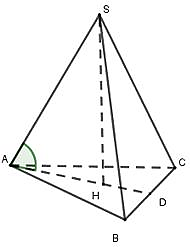
Gọi H là trọng tâm tam giác ABC.

Vì S.ABC là hình chóp tam giác đều nên SH ^ (ABC).

Gọi D là trung điểm của BC nên  $AH=\frac{2}{3}AD$.

Vì AD là đường trung tuyến trong tam giác ABC đều cạnh a nên  $AD=\frac{a\sqrt{3}}{2}$.

$\Rightarrow AH=\frac{2}{3}AD=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$.

Ta có SH ^ (ABC).

Suy ra góc giữa cạnh bên SA và đáy là góc giữa SA và AH, hay là  $\widehat{SAH}$.

Theo đề bài ta có:  $\widehat{SAH}=45°$ nên suy ra ∆SAH vuông cân tại H.

Khi đó  $SH=AH=\frac{a\sqrt{3}}{3}$

Diện tích tam giác ABC đều cạnh a là  $\frac{a^2\sqrt{3}}{4}$

Thể tích khối chóp là:

$V_{S.ABC}=\frac{1}{3}SH.S_{ABC}=\frac{1}{3}.\frac{a\sqrt{3}}{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3}{12}$