Ông Bình đặt thợ làm một bể cá, nguyên liệu bằng kính trong suốt, không có

Câu 1:

Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số $g_1\left(x\right)=4x+1,g_2\left(x\right)=x+2,g_3\left(x\right)=-2x+4$. Giá trị lớn nhất của f(x) trên R là:

Xem lời giải »

Câu 2:

Biết rằng đồ thị của hàm số $y=P\left(x\right)=x^3-2x^2-5x+2$ cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là $x_1,x_2,x_3$. Khi đó giá trị của biểu thức $T=\frac{1}{x_1^2-4x_1+3}+\frac{1}{x_2^2-4x_2+3}+\frac{1}{x_3^2-4x_3+3}$ bằng:

Xem lời giải »

Câu 3:

Cho hàm số y = f(x) có bảng biến thiên như sau:

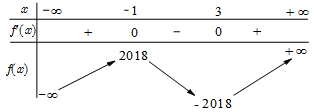
Đồ thị hàm số $y=\left|f\left(x-2017\right)+2018\right|$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 4:

Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy đến hòn đảo C (như hình vẽ). Biết rằng chi phí đi đường thủy là 5USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.

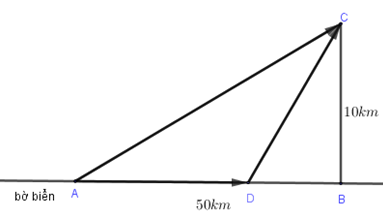
Xem lời giải »

Câu 5:

Cho hàm số $y=x^4-2m{x}^2+m$ có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến $∆$ với đồ thị (C) tại A cắt đường tròn $\left(\gamma \right):x^2+{\left(y-1\right)}^2=4$ tạo thành một dây cung có độ dài nhỏ nhất

Xem lời giải »

Câu 6:

Cho hàm số f(x) có đồ thị hàm đường cong (C), biết đồ thị của f'(x) như hình vẽ:

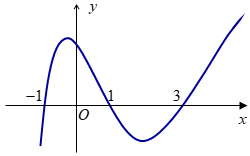
Tiếp tuyến của (C ) tại điểm có hoành độ bằng 1 cắt đồ thị (C ) tại hai điểm A, B phân biệt lần lượt có hoành độ a, b. Chọn khẳng định đúng trong các khẳng định sau:

Xem lời giải »

Câu 7:

Cho hàm số $y={\left(x-m\right)}^3-3x+m^2$ có đồ thị là $\left(C_m\right)$ với m là tham số thực. Biết điểm M(a; b) là điểm cực đại của $\left(C_m\right)$ ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của $\left(C_m\right)$ ứng với một giá trị khác của m. Tổng $S=2018a+2020b$ bằng:

Xem lời giải »

Câu 8:

Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị $y=-x^3+6x^2-9x+2$ tại 3 điểm phân biệt A, B, C. Gọi B’, C’ lần lượt là hình chiếu vuông góc của B, C lên trục tung. Tìm giá trị dương của m để hình thang BB’C’C có diện tích bằng 8.

Xem lời giải »