Tính diện tích của 1 tam giác cân có chiều cao ứng với cạnh đáy bằng 10 cm, chiều cao ứng với cạnh bên bằng 12 cm.
Câu hỏi:
Tính diện tích của 1 tam giác cân có chiều cao ứng với cạnh đáy bằng 10 cm, chiều cao ứng với cạnh bên bằng 12 cm.
Trả lời:
Lời giải
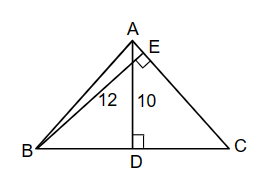
Gọi tam giác cân là ABC (cân tại A), đường cao AD và BE
Gọi cạnh đáy của tam giác cân là a, cạnh bên là b
Ta có \({S_{ABC}} = \frac{1}{2}a.10 = \frac{1}{2}b.12\)
Suy ra 10a = 12b
Hay \(\frac{a}{b} = \frac{6}{5}\)
Đặt a = 6k, b = 5k
Xét tam giác ADC vuông tại D có
AD2 + DC2 = AC2
\( \Leftrightarrow {10^2} + {\left( {\frac{a}{2}} \right)^2} = {b^2}\)
\( \Leftrightarrow {10^2} + {\left( {\frac{{6k}}{2}} \right)^2} = {\left( {5k} \right)^2}\)
⇔ 100 + 9k2 = 25k2
⇔ 100 = 16k2
\( \Leftrightarrow k = \frac{{10}}{4}\)
Suy ra a = 6k = 15 (cm)
Ta có \({S_{ABC}} = \frac{1}{2}a.10 = \frac{1}{2}.15.10 = 75\) (cm2).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Gọi D là trung điểm của AB, E là trọng tâm tam giác ACD. Chứng minh rằng OE vuông góc với CD.
Xem lời giải »
Câu 2:
Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \[{\rm{A}}M = \frac{{AC}}{4}\]. Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).
Xem lời giải »
Câu 3:
Cho hình vuông ABCD có cạnh bằng 2. Tính \(T = \left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).
Xem lời giải »
Câu 4:
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.
a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Giả sử BC = 2a. Tính BM . CN.
d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Xem lời giải »
Câu 5:
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC, biết OB = 2cm và OA = 4cm.
Xem lời giải »
Câu 6:
Cho 3 đường thẳng: d1: y= mx – m + 1; d2: y = 2x + 3; d3: y = x + 1.
a) Chứng minh rằng khi m thay đổi, đường thẳng d1 luôn đi qua 1 điểm cố định.
b) Tìm m để 3 đường thẳng trên đồng quy. Tính tọa độ điểm giao nhau đó.
Xem lời giải »
Câu 7:
Cho đường thẳng d: y = 2x + 6 cắt Ox; Oy theo thứ tự A và B. Diện tích tam giác OAB là:
Xem lời giải »
Câu 8:
Tìm các số nguyên n sao cho 2n3 + n2 + 7n + 1 chia hết cho 2n – 1.
Xem lời giải »


