Trong không gian, cho hình thang cân ABCD có AB // CD, AB = a, CD = 2a

Câu hỏi:

Trong không gian, cho hình thang cân ABCD có AB // CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần S_ep của khối K.

Trả lời:

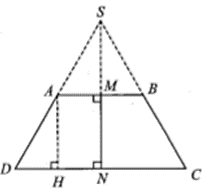
Media VietJack

Gọi S là giao điểm của AD và BC

Nếu quay tam giác SCD quanh trục SN, các đoạn thẳng SC, SB lần lượt tạo ra mặt xung quanh cảu hình nón (H₁) và (H₂).

Với hình nón (H₁):

$l_{1} = S C = 2 a, r_{1} = N C = a, h_{1} = S N = a \sqrt{3}$

Với hình nón (H₂):

$l_{2} = S B = a, r_{2} = M B = \frac{a}{2}, h_{2} = S M = \frac{a \sqrt{3}}{2}$

Diện tích xung qunah của khối tròn xoay là:

S_{x q} = S_{(H_{1})} - S_{(H_{2})} = π l_{1} r_{1} - π l_{2} r_{2}

= 2 π a^{2} - \frac{π a^{2}}{2} = \frac{3 π a^{2}}{2}

Diện tích hai đáy:

S_đáy = S₁ + S₂ = pr₁² + pr₂²

^{$= π a^{2} + \frac{π a^{2}}{4} = \frac{5 π a^{2}}{4}$}

Suy ra $S_{t p} = \frac{3 π a^{2}}{2} + \frac{5 π a^{2}}{4} = \frac{11 π a^{2}}{4}$ .

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tính giá trị lớn nhất của hàm số y = x(2 − ln x) trên đoạn [2; 3].

Xem lời giải »

Câu 2:

Tìm giá trị nhỏ nhất của hàm số y = x²ln x trên đoạn [1; 2].

Xem lời giải »

Câu 3:

Hàm số y = cos 2x đồng biến trên khoảng nào?

Xem lời giải »

Câu 4:

Hàm số y = cos 2x nghịch biến trên khoảng nào sau đây (k Î ℤ).

Xem lời giải »

Câu 5:

Cho tam giác ABC vuông cân tại A, BC = a. Quay hình tròn ngoại tiếp tam giác vuông ABC xung qunah cạnh BC ta được một khối tròn xoay có thể tích bằng:

Xem lời giải »

Câu 6:

Cho tam giác ABC cân tại A, góc $\hat{B A C} = 120 °$ và AB = 4 cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.

Xem lời giải »

Câu 7:

Cho hình chóp S.ABCD. Gọi M là trung điểm SB, N thuộc SC sao cho SN = 2NC. Tìm giao điểm của SA và mp (DMN).

Xem lời giải »

Câu 8:

Cho hình chóp S.ABCD, gọi M là trung điểm SB và N là điểm thuộc cạnh SC sao cho SN = 2NC. Tính tỉ số $\frac{V_{S . A M N}}{V_{S . A B C}}$ .

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Trong không gian, cho hình thang cân ABCD có AB // CD, AB = a, CD = 2a

Xem thêm bài tập Toán có lời giải hay khác: