Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G, H lần
Câu hỏi:
Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, AD. Tính diện tích tứ giác EFGH, biết AC = 8cm và BD = 6cm.
Trả lời:
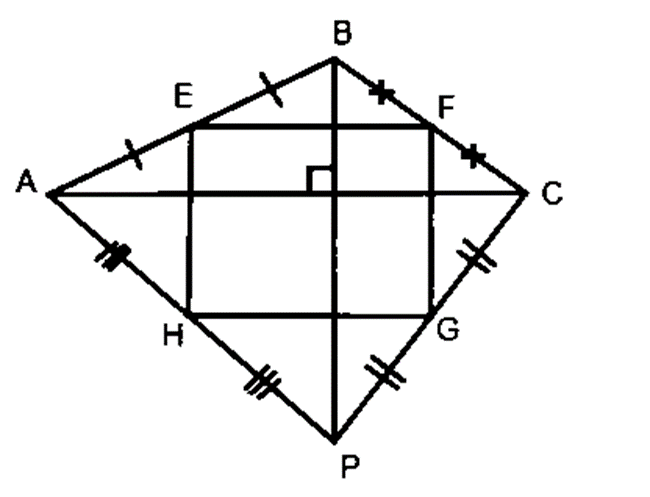
Ta có EF, HG lần lượt là các đường trung bình của ΔABC và ΔADC nên EF // HG // AC
EF // HG và EF = HG. Do đó tứ giác EFGH là hình bình hành.
Tương tự EH // BD mà BD ⊥ AC (gt)
⇒ EF ⊥ EH
Do đó EFGH là hình chữ nhật và EF = \(\frac{1}{2}AC = 4cm,EH = \frac{1}{2}BD = 3cm\).
Vậy SEFGH = EF.EH = 12 (cm2).

