Cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm
Câu hỏi:
Cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D. Gọi K là giao điểm của EB với đường tròn (O) và H là giao điểm của BD và AK.
a) ΔABE là tam giác gì?
b) Chứng minh rằng EH vuông góc với AB.
c) Chứng minh rằng OD vuông góc với AK.
Trả lời:
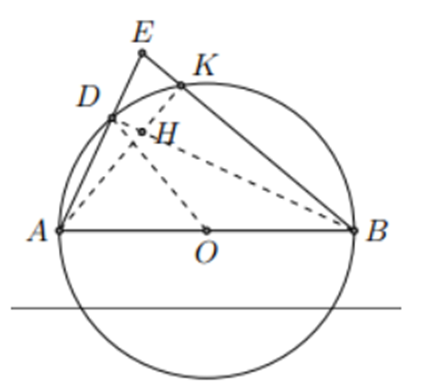
a) Xét tam giác ABE có: \(\widehat {ADB} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Suy ra: BD ⊥ AE (1)
Tức là BD là trung tuyến vừa là đường cao
Do đó: Tam giác ABE cân tại B
b) Ta có: \(\widehat {AKB} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Suy ra: AK ⊥ BE (2)
Từ (1) và (2): H là trực tâm của ∆ABE
Suy ra: EH ⊥ AB
c) Ta có: AK ⊥ KB (phần b)
Suy ra: AK ⊥ EB (*)
Lại có: D là trung điểm của AE (vì E là điểm đối xứng với A qua D )
O là trung điểm của AB ( vì AB là đường kính)
Do đó OD//EB (**)
Từ (*) và (**) suy ra: OD ⊥ AK .

