Cho tam giác ABC nội tiếp đường tròn (O); phân giác AD. Vẽ đường tròn (O') đi
Câu hỏi:
Cho tam giác ABC nội tiếp đường tròn (O); phân giác AD. Vẽ đường tròn (O') đi qua A, D và tiếp xúc với (O). Gọi M, N là giao của AB, AC với (O'). Chứng minh rằng:
a) MN song song với BC.
b) BC là tiếp tuyến của (O').
Trả lời:
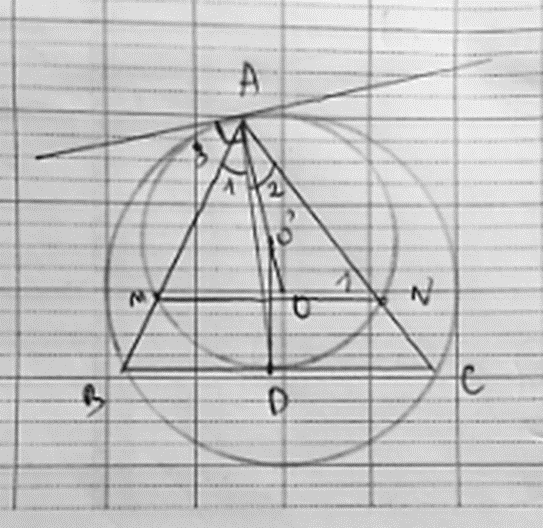
a) Đường tròn O có ABC nội tiếp nên \[\widehat {{A_3}} = \widehat C\] (chắn cung AB)
Đường tròn O' có AMN nội tiếp nên \[\widehat {{A_3}} = \widehat {{N_1}}\] (chắn cung AM)
Do đó \[\widehat C = \widehat {{N_1}}\] suy ra MN // BC
b) Ta có: \(\widehat {ADB} = \widehat {{A_2}} + \widehat C\)( góc ngoài tam giác ADC)
mà \[\widehat {{A_3}} = \widehat C\] và \[\widehat {{A_1}} = \widehat {{A_2}}\]
Do đó \[\widehat {ADB} = \widehat {{A_3}} + \widehat {{A_1}}\]
Lại có tam giác O'AD cân tại O' nên \(\widehat {O'AD} = \widehat {O'DA}\)
Do đó \(\widehat {O'AD} + \widehat {{A_3}} + \widehat {{A_1}} = \widehat {O'DA} + \widehat {BDA}\) hay \(90^\circ = \widehat {O'DA} + \widehat {BDA}\)
Suy ra: \(\widehat {O'DB} = 90^\circ \)
Vậy BC là tiếp tuyến của (O’).

