Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y= x^3+mx-1/5x^5
Câu hỏi:
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số đồng biến với x > 0?
Trả lời:
+ Hàm số xác định và liên tục với mọi x > 0.
Ta có
+ Hàm số đồng biến trên khoảng (0; +∞) khi và chỉ khi:
Xét
Bảng biến thiên:
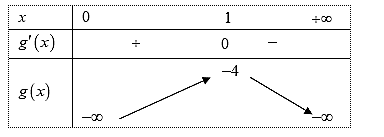
Suy ra max g (x) = g (1) = −4 và do đó để hàm số đã cho đồng biến t với x > 0 thì m ≥ −4
Mà m nguyên âm nên m Î{−4; −3; −2; −1}.
Vậy có 4 giá trị nguyên âm của tham số m thỏa mãn.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tính giá trị lớn nhất của hàm số y = x(2 − ln x) trên đoạn [2; 3].
Xem lời giải »
Câu 2:
Tìm giá trị nhỏ nhất của hàm số y = x2ln x trên đoạn [1; 2].
Xem lời giải »
Câu 4:
Hàm số y = cos 2x nghịch biến trên khoảng nào sau đây (k Î ℤ).
Xem lời giải »
Câu 5:
Tìm giá trị thực của tham số m để đường thẳng d: y = (2m − 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 1.
Xem lời giải »
Câu 6:
Tìm giá trị thực của tham số m để đường thẳng d: y = (3m + 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 − 1.
Xem lời giải »
Câu 8:
Cho hàm số f (x) có đạo hàm f ¢(x) = x(x + 2)2, "x Î ℝ. Số điểm cực trị của hàm số đã cho là:
Xem lời giải »


